Realizar un forecast es una tarea que generalmente requiere de conocimiento del sector, hipotetizar sofre efectos que afecten al resultado de estudio y como no, tener unas mínimas habilidades de programación.
En siguiente ejemplo, utilizo los datos de la CNMC del informe de supervisión de cambio de comercializador, donde se publican trimestralmente multitud de indicadores del sector eléctrico y gasista en cuanto a altas, switchings y movilidad entre grupos comercializadores.
La información publicada es de gran calidad, pero los datos ciertamente no están en el mejor formato: leer un excel de 58 pestañas no es en absoluto práctico, por lo que trabajaré sobre la tabla de datos correspondiente al histórico de puntos de suministros desglosado por grupos comercializadores del mercado libre vs mercado regulado, para el sector doméstico (donde las no-incumbentes quedan agrupadas bajo la categoría “Otros”).
## # A tibble: 63 x 14
## MES `CHC Libre` `CHC COR` `EDP Libre` `EDP COR` `END Libre` `END COR`
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2013… 431704. NA 533669. 273782. 2500277. 8509767.
## 2 2013… 431580. NA 540284. 271704. 2537298. 8450201.
## 3 2013… 430928. NA 548418. 269503. 2591980. 8383955.
## 4 2013… 430889. NA 555814. 267857. 2642513. 8318347.
## 5 2013… 430952. NA 566185. 268035. 2715919. 8243974.
## 6 2013… 430588. NA 576115. 264142. 2813246. 8145236.
## 7 2013… 429623. NA 582699. 263496. 2901920. 8048981.
## 8 2013… 430092. NA 586615. 262441. 2976211. 7973733.
## 9 2013… 428856. NA 591374. 261774. 3074063. 7859033.
## 10 2013… 428859. NA 597184. 258720. 3156578. 7787221.
## # ... with 53 more rows, and 7 more variables: `GNF Libre` <dbl>, `GNF
## # COR` <dbl>, `IB Libre` <dbl>, `IB COR` <dbl>, `Viesgo Libre` <dbl>,
## # `Viesgo COR` <dbl>, Otros <dbl>Análisis exploratorio
Los datos muestran, para el sector doméstico, la evolución de los puntos de suministro o CUPS pertenecientes a cada grupo comercializador incumbente, tanto para su comercializadora libre como para la regulada, y agrupa bajo el título Otros, a los independientes. Lo que se desea es aplicar un sencillo forecast de la cantidad de CUPS que puede haber de aquí a un par de años en el mercado regulado, por lo que en primer lugar, prepararé la tabla para transformarla en un time-series que pueda trabajar con el paquete forecast de Rob J.Hyndman.
# Transformación a timeseries
historico_ts <- historico %>% replace(is.na(.), 0) %>%
mutate(COR = `CHC COR` + `EDP COR` + `END COR` + `GNF COR` + `IB COR` + `Viesgo COR`,
TOTAL = `CHC COR` + `EDP COR` + `END COR` + `GNF COR` + `IB COR` + `Viesgo COR` +
`CHC Libre` + `EDP Libre` + `END Libre` + `GNF Libre` + `IB Libre` + Otros,
porcentaje_COR = (COR / TOTAL) * 100) %>%
select(porcentaje_COR) %>%
ts(start = c(2013, 1), end = c(2018, 3), frequency = 12)
historico_ts ## Jan Feb Mar Apr May Jun Jul
## 2013 64.16329 63.56927 62.94927 62.42375 61.81661 61.15076 60.50228
## 2014 56.46784 55.83724 55.11964 54.39769 53.88916 53.32136 52.78567
## 2015 50.41908 50.08115 49.67745 49.32799 48.95173 48.58362 48.24962
## 2016 46.32585 46.04070 45.73555 45.45764 45.21055 44.98165 44.77481
## 2017 43.52676 43.24856 42.95622 42.73558 42.51335 42.31269 42.12424
## 2018 41.06766 40.92544 40.79288
## Aug Sep Oct Nov Dec
## 2013 59.95495 59.31933 58.64294 57.84764 57.10442
## 2014 52.37887 51.98239 51.55223 51.10097 50.74261
## 2015 47.94407 47.61929 47.28256 46.94032 46.57169
## 2016 44.55934 44.36882 44.16731 43.95493 43.77685
## 2017 41.96470 41.84225 41.67052 41.47096 41.29500
## 2018Graficando la tabla se observa que la función no debe ser en absoluto compleja. Es más, intuitivamente uno podría deducir el % de suministros remanentes del mercado regulado de aquí a cinco años, asumiendo que no existirá cambio normativo mediante, ni efectos no previstos en captación por parte de las no incumbentes. El objetivo de este tutorial no es realizar complejos forecasts, sino aplicar la teoría más básica del paquete del profesor Hyndman.
# Time series
autoplot(historico_ts) +
ggtitle("Evolución de % CUPS en mercado regulado") +
xlab("mes") +
ylab("% CUPS") +
scale_y_continuous(labels = function(x) format(x, scientific = FALSE))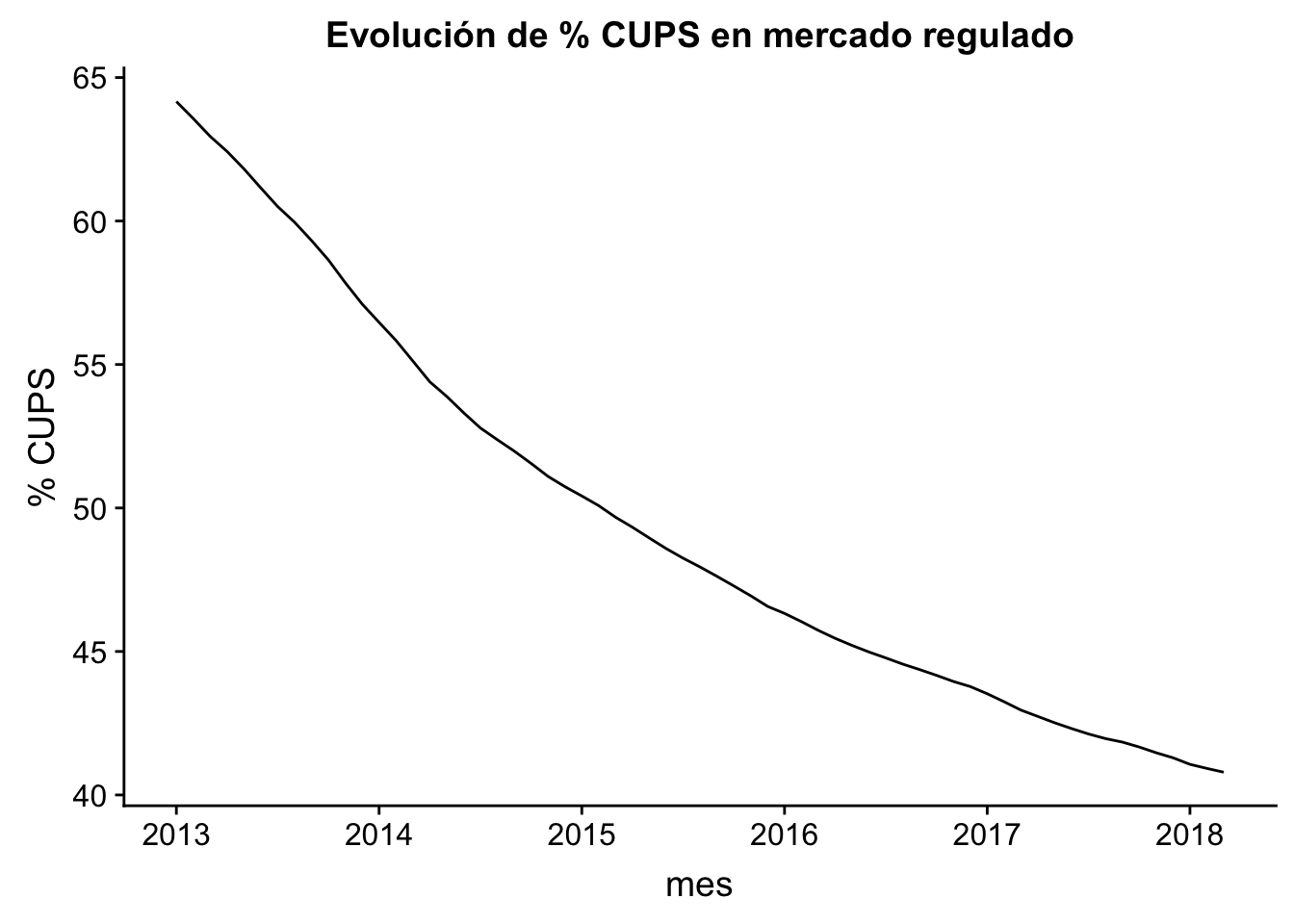
# Seasonal time series
ggseasonplot(historico_ts, year.labels=TRUE, year.labels.left=TRUE) +
ylab("% CUPS") +
ggtitle("Evolución de % CUPS en mercado regulado por año") +
scale_y_continuous(labels = function(x) format(x, scientific = FALSE))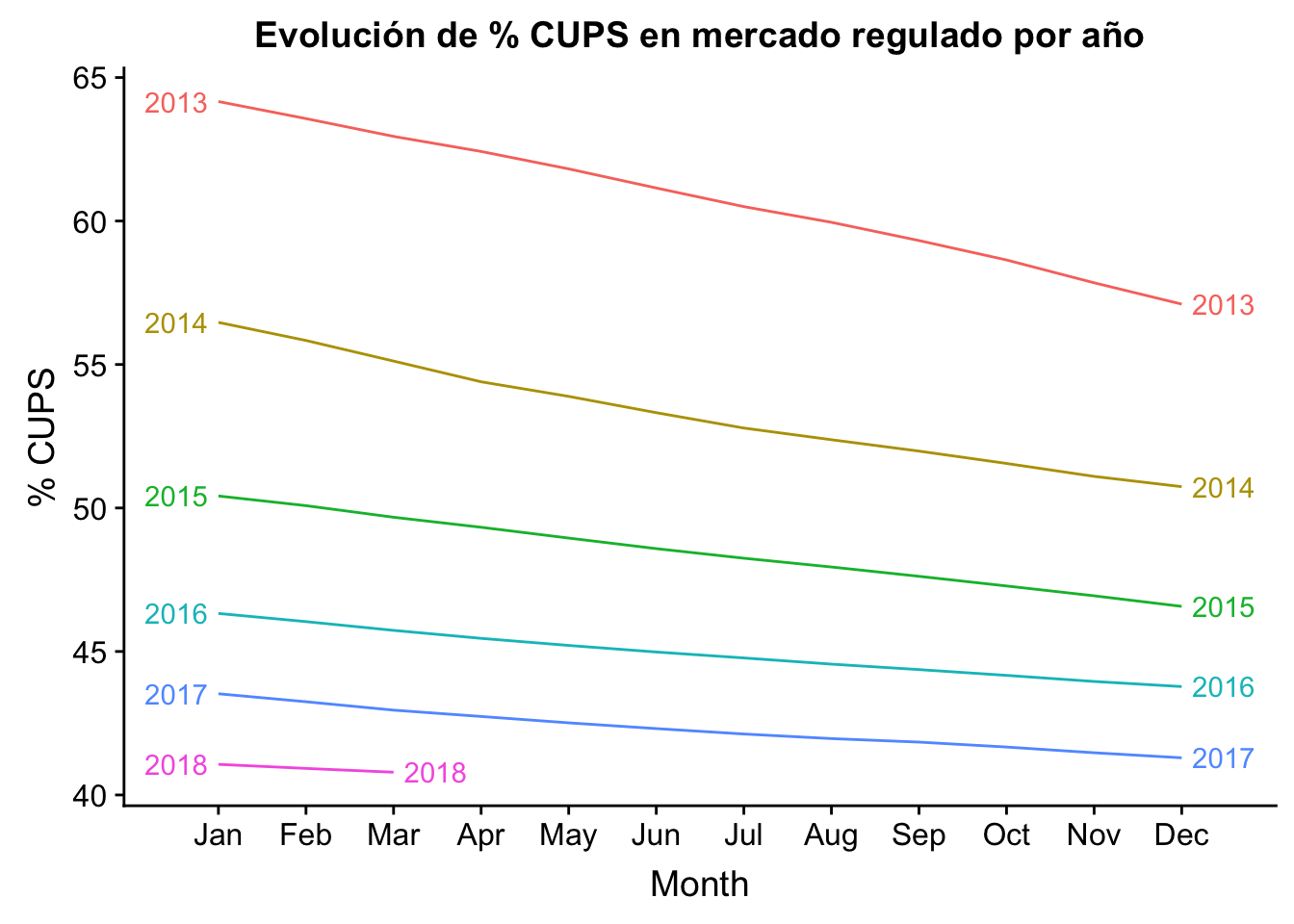
Características del time series
Para cualquier serie temporal (time series) hay 3 características o patrones que deben ser analizados:
Tendencia: existe cuando se detecta un incremento o decremento a lo largo del tiempo. En este caso, es claro que existe una tendencia negativa, ya que el % de CUPS disminuye con el tiempo.
Estacionalidad: existe cuando la serie temporal se ve afectada por patrones estacionales (anuales, mensuales, semanales, horarios), fruto de una frecuencia fija. En este caso, no existe dicho efecto.
Ciclo: existe cuando se dan incrementos o decrementos en los datos que no son fruto de la frecuencia fija. En este caso, tampoco se exhibe dicho efecto.
Lag plots: gráficos de dispersión del valor yt vs valor con desfase yt-k
Este tipo de gráficos muestran la relación existente entre los valores de la serie temporal y ese mismo valor con un lag o desfase determinado. En este caso se llega a comparar cada valor con el correspondiente desde un lag = 1, hasta un lag = 16.
gglagplot(historico_ts)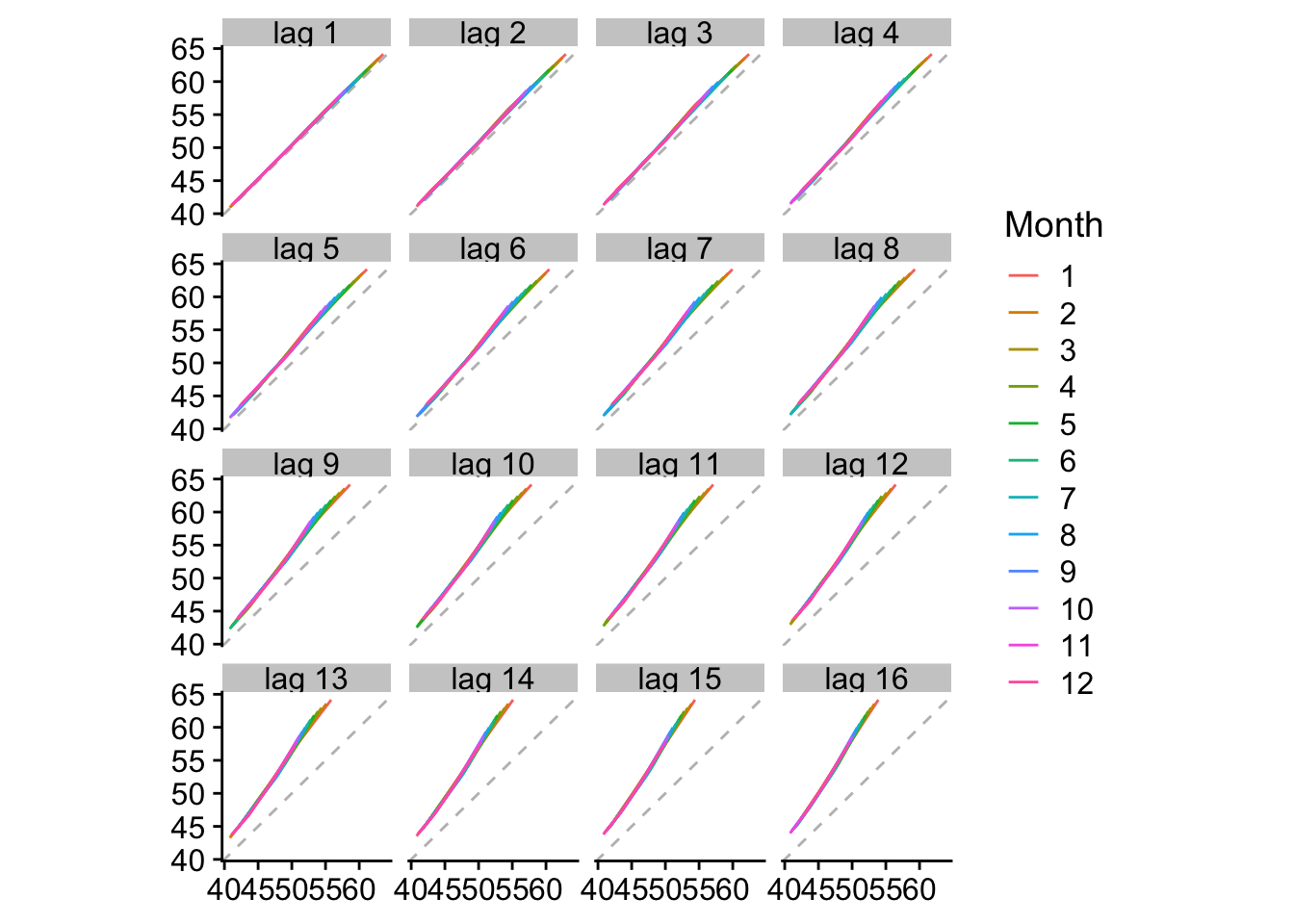
Se observa la linealidad en todos, debido a que para nivel (mes) no existe estacionalidad, pero se observa un efecto curioso: la relación lineal es mayor conforme más pequeño es el lag, es decir, conforme más reciente es el valor a comparar.
Forecast para benchmark
A continuación he realizado 3 forecast simples para los próximos 2 años:
Media: el forecast de los valores futuros es la media de los valores pasados. Simple, ¿verdad?
Naïve: el forecast se corresponde con el último valor observado. También simple, ¿verdad?
Drift Naïve: se permite que el forecast Naïve pueda tener tendencia igual a la media del decremento (en este caso) histórico.
autoplot(historico_ts) +
autolayer(meanf(historico_ts, h=24),
series="Mean", PI=FALSE) +
autolayer(rwf(historico_ts, h=24),
series="Naïve", PI=FALSE) +
autolayer(rwf(historico_ts, drift=TRUE, h=24),
series="Drift", PI=FALSE) +
ggtitle("Forecast % CUPS mercado regulado") +
xlab("Mes") + ylab("% CUPS") +
guides(colour=guide_legend(title="Forecast"))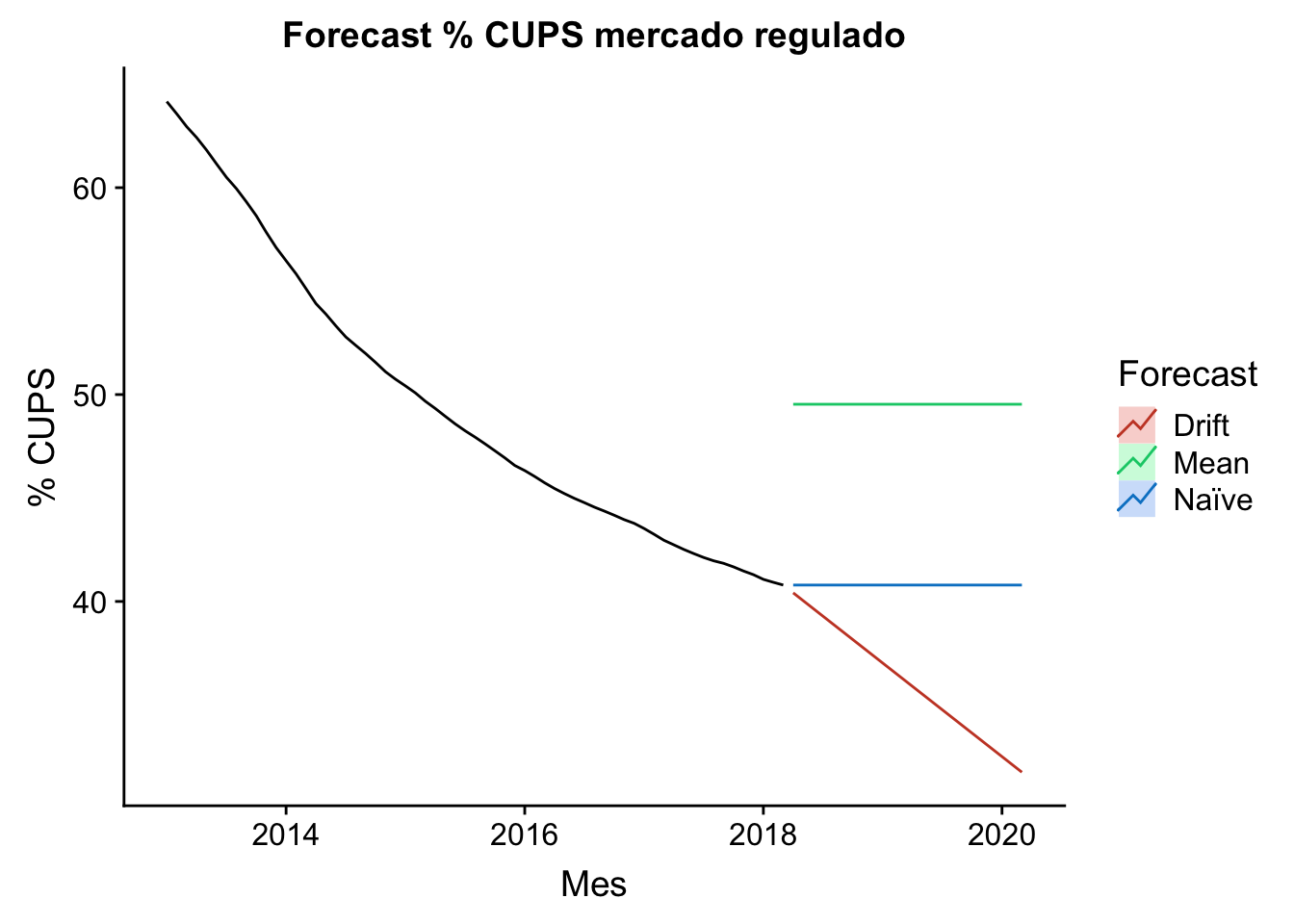
Análisis de los residuos
Tomando como ejemplo, el método Naïve drift, el obligatorio analizar los residuos del modelo:
checkresiduals(rwf(historico_ts, drift = TRUE))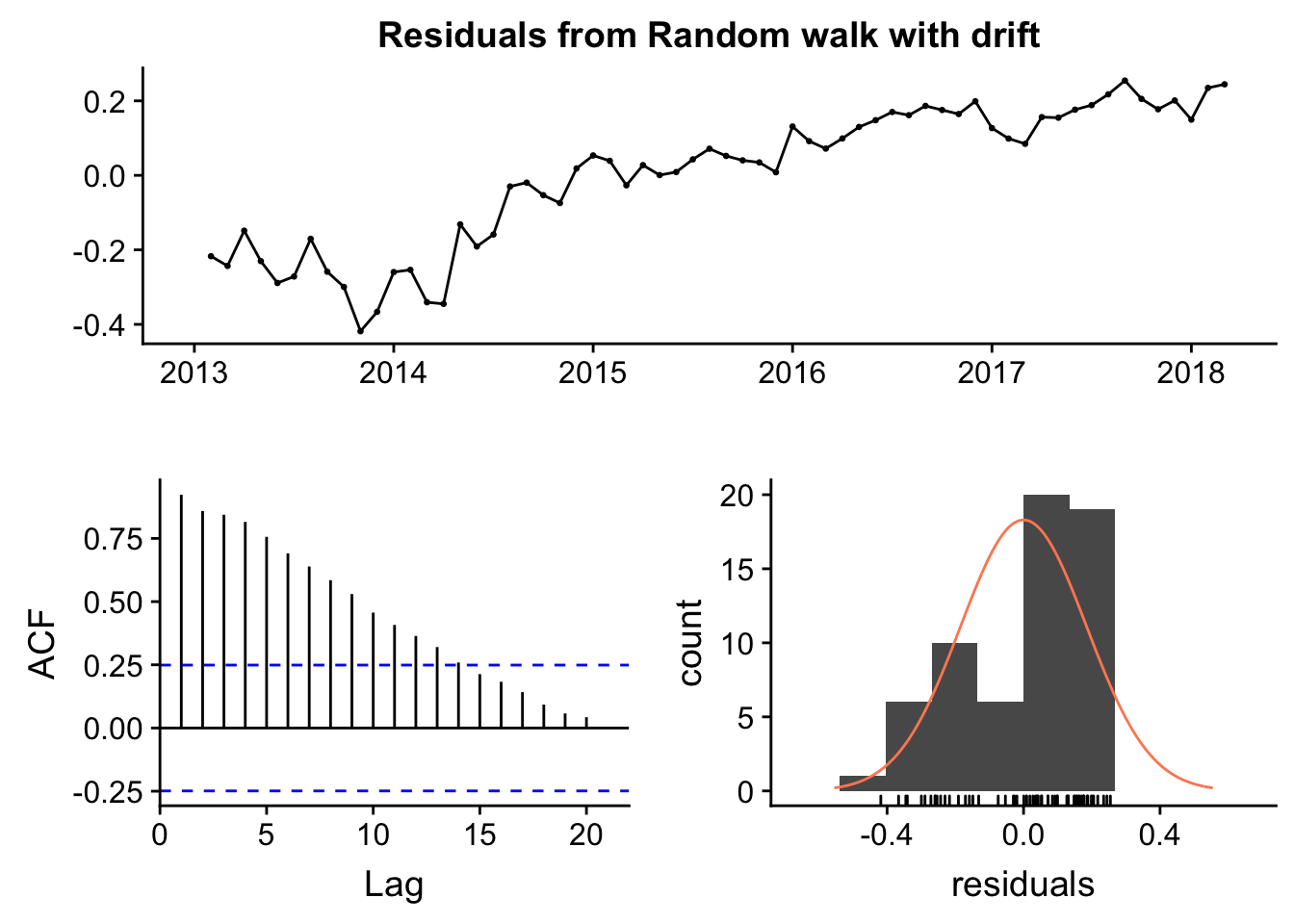
##
## Ljung-Box test
##
## data: Residuals from Random walk with drift
## Q* = 410.87, df = 23, p-value < 2.2e-16
##
## Model df: 1. Total lags used: 24El test de Ljung-Box comprueba si nuestros datos son distinguibles o no de ruido blanco (series temporales sin autocorrelación): como el p-valor es significativo, concluimos que existe evidencia para rechazar dicha hipótesis.
El primer gráfico muestra los residuos, es decir, la diferencia entre los valores ajustados y los reales. Se observa una tendencia, lógico por otra parte, ya que el modelo lo que está haciendo es fijar una recta sobre nuestra serie de datos: se queda corto por un extremo y largo por el opuesto.
El segundo gráfico muestra el ACF (autocorrelation function) muestra el correlograma de los datos. Todo las líneas que están por encima o por debajo de las líneas azules de puntos, indican que existen correlaciones significativas de los puntos con sus versiones laggeadas. Como ya indicaba el lag plot, la correlación es más intensa a valores más próximos entre sí.
El tercero muestra el histograma de distribución de los residuos, que idóneamente debería seguir una distribución normal (supuesto que no cumple).
Dos tipos de forecast
Probaré a realizar el forecast a 2 años mediante dos métodos: el de Holt y el ARIMA. Idóneamente, cualquier tipo de modelización se debe hacer en base a training set y un test set: el modelo aprenderá de los datos del train set, y predecirá el tramo correspondiente al test set. Lógicamente, se compararía después cómo de bien lo ha hecho calculando el error producido entre los valores predichos y los reales del test set.
Sin embargo, dada la simplicidad del set de datos, haré directamente el forecast a 2 años para ver si las diferencias entre los dos métodos son significativas o no.
Forecast mediante el método de Holt
El método de Holt es un suavizado exponencial, adecuado cuando se tienen series temporales donde se quiere que la tendencia sea tenida en cuenta. Los métodos benchmark anteriores eran planos, con pendiente nula para el método de la media y el Naïve. Ahora, la tendencia será tenida en cuenta con el método Holt, y su respectiva variante amortiguada, que aplicará una tendencia no constante:
# Comparación entre ambos métodos Holt
fc <- holt(historico_ts, h=24)
fc2 <- holt(historico_ts, damped=TRUE, h=24)
# Gráfico
autoplot(historico_ts) +
autolayer(fc, series="Método Holt", PI=FALSE) +
autolayer(fc2, series="Método amortiguada Holt", PI=FALSE) +
ggtitle("Forecasts con el método Holt") + xlab("mes") +
ylab("% CUPS") +
guides(colour=guide_legend(title="Forecast"))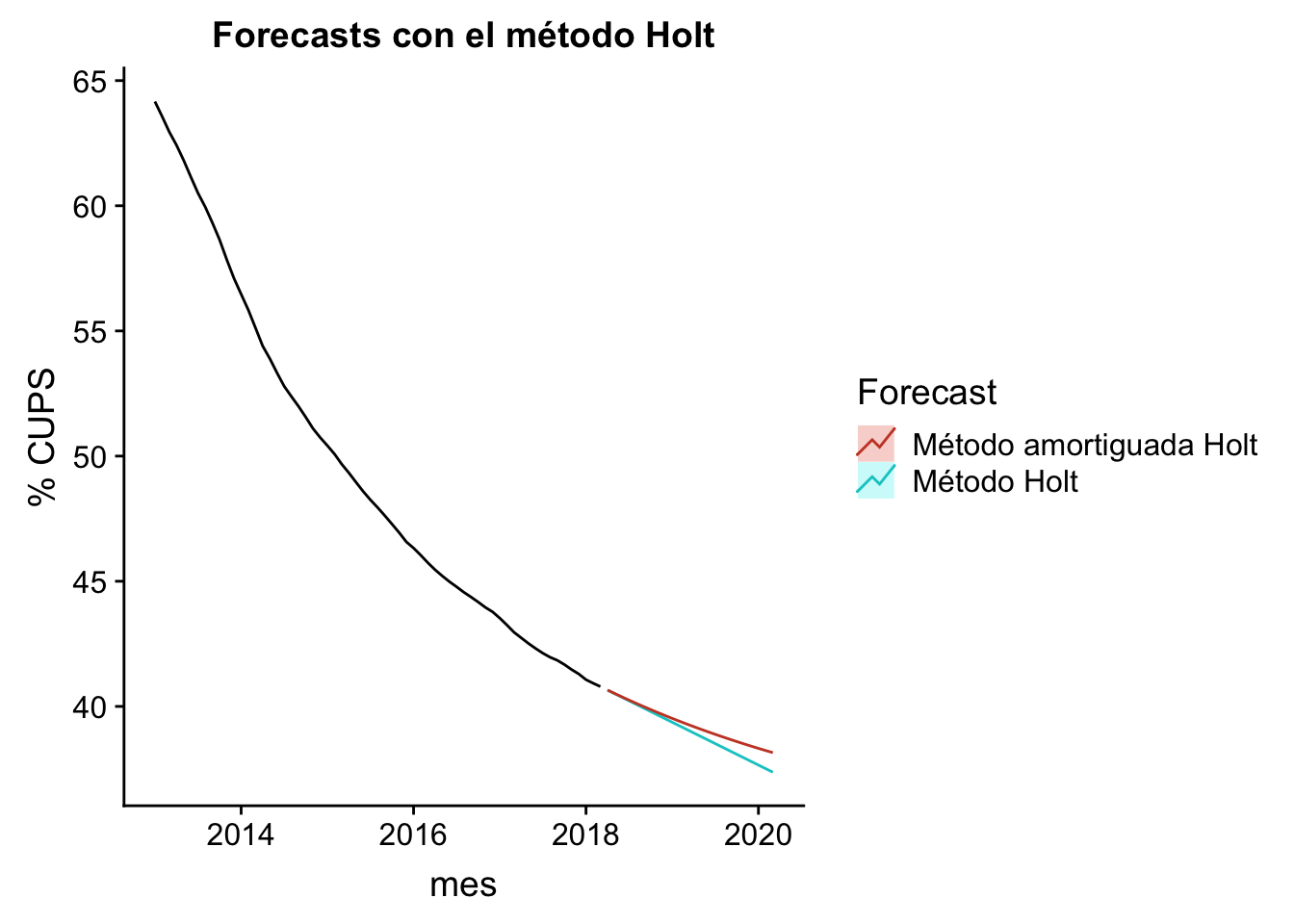
# Forecast elegido
autoplot(fc2)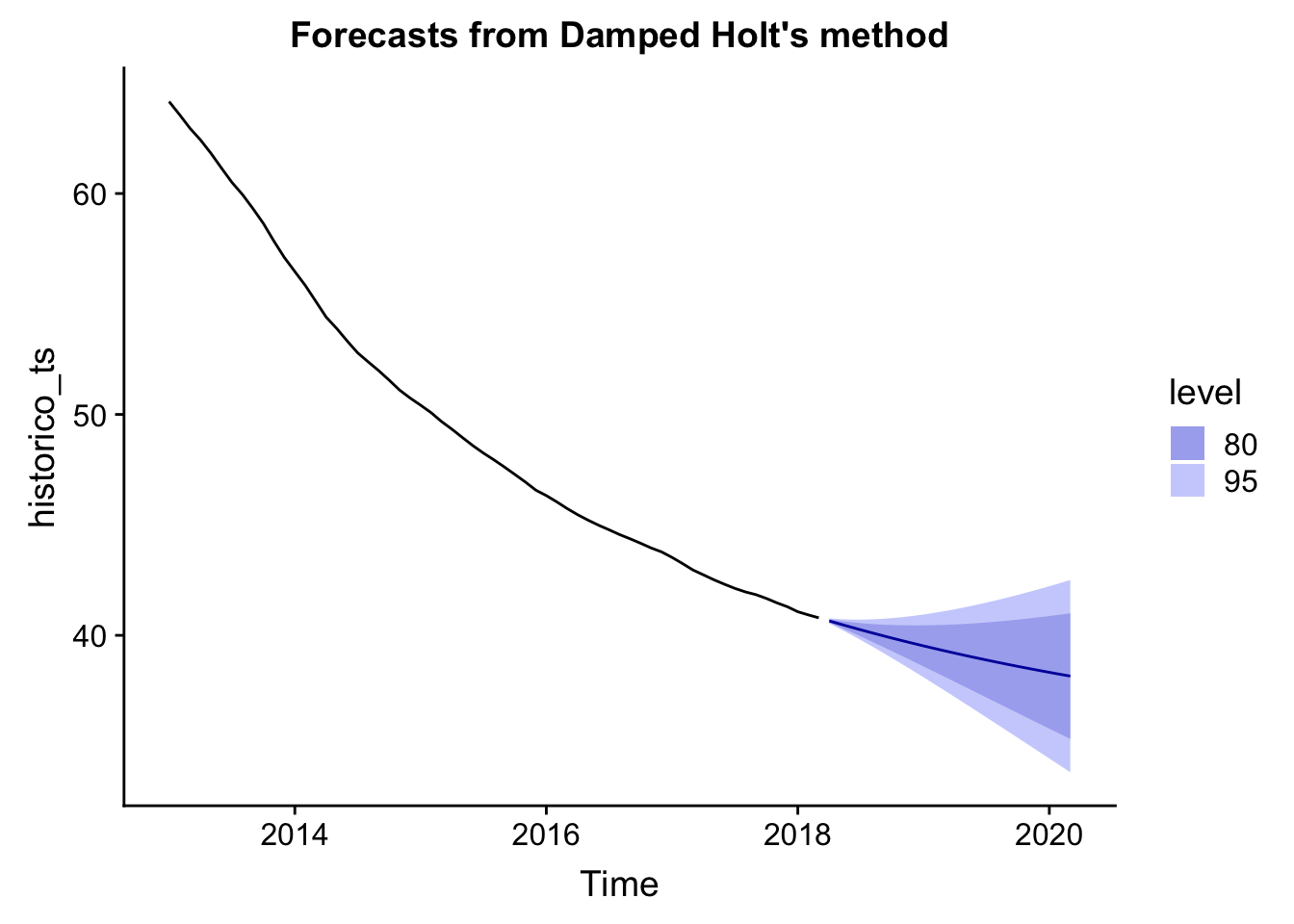
# Tabla de datos del forecast
fc2## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## Apr 2018 40.65278 40.57835 40.72720 40.53895 40.76660
## May 2018 40.51574 40.37449 40.65698 40.29972 40.73175
## Jun 2018 40.38169 40.16473 40.59864 40.04988 40.71349
## Jul 2018 40.25056 39.94977 40.55135 39.79055 40.71058
## Aug 2018 40.12230 39.73052 40.51409 39.52312 40.72149
## Sep 2018 39.99685 39.50773 40.48596 39.24881 40.74489
## Oct 2018 39.87413 39.28204 40.46622 38.96860 40.77966
## Nov 2018 39.75409 39.05396 40.45422 38.68334 40.82484
## Dec 2018 39.63668 38.82395 40.44940 38.39372 40.87964
## Jan 2019 39.52182 38.59236 40.45129 38.10033 40.94332
## Feb 2019 39.40948 38.35952 40.45944 37.80371 41.01526
## Mar 2019 39.29959 38.12571 40.47348 37.50429 41.09489
## Apr 2019 39.19210 37.89116 40.49304 37.20248 41.18172
## May 2019 39.08696 37.65609 40.51783 36.89863 41.27528
## Jun 2019 38.98411 37.42069 40.54754 36.59306 41.37516
## Jul 2019 38.88351 37.18512 40.58190 36.28605 41.48097
## Aug 2019 38.78511 36.94954 40.62068 35.97785 41.59237
## Sep 2019 38.68886 36.71408 40.66363 35.66869 41.70902
## Oct 2019 38.59470 36.47885 40.71056 35.35879 41.83062
## Nov 2019 38.50261 36.24397 40.76125 35.04832 41.95690
## Dec 2019 38.41253 36.00954 40.81552 34.73747 42.08758
## Jan 2020 38.32441 35.77563 40.87319 34.42639 42.22243
## Feb 2020 38.23822 35.54233 40.93410 34.11522 42.36121
## Mar 2020 38.15391 35.30972 40.99809 33.80410 42.50371Se ve claramente que el método amortiguado conporta una tendencia no constante, quizás más realista que el método Holt lineal.
Forecast mediante ARIMA
El método ARIMA es un método tremendamente flexible, que se basa en la autocorrelación de los datos de la serie temporal. Requiere un trabajo y esfuerzo considerables parametrizar el modelo para minimizar el error, pero ahora comprobaré con una parametrización automática que lleva a cabo la función auto.arima:
# Forecast ARIMA
fc_arima <- historico_ts %>% auto.arima() %>% forecast()
# Gráfico
autoplot(fc_arima)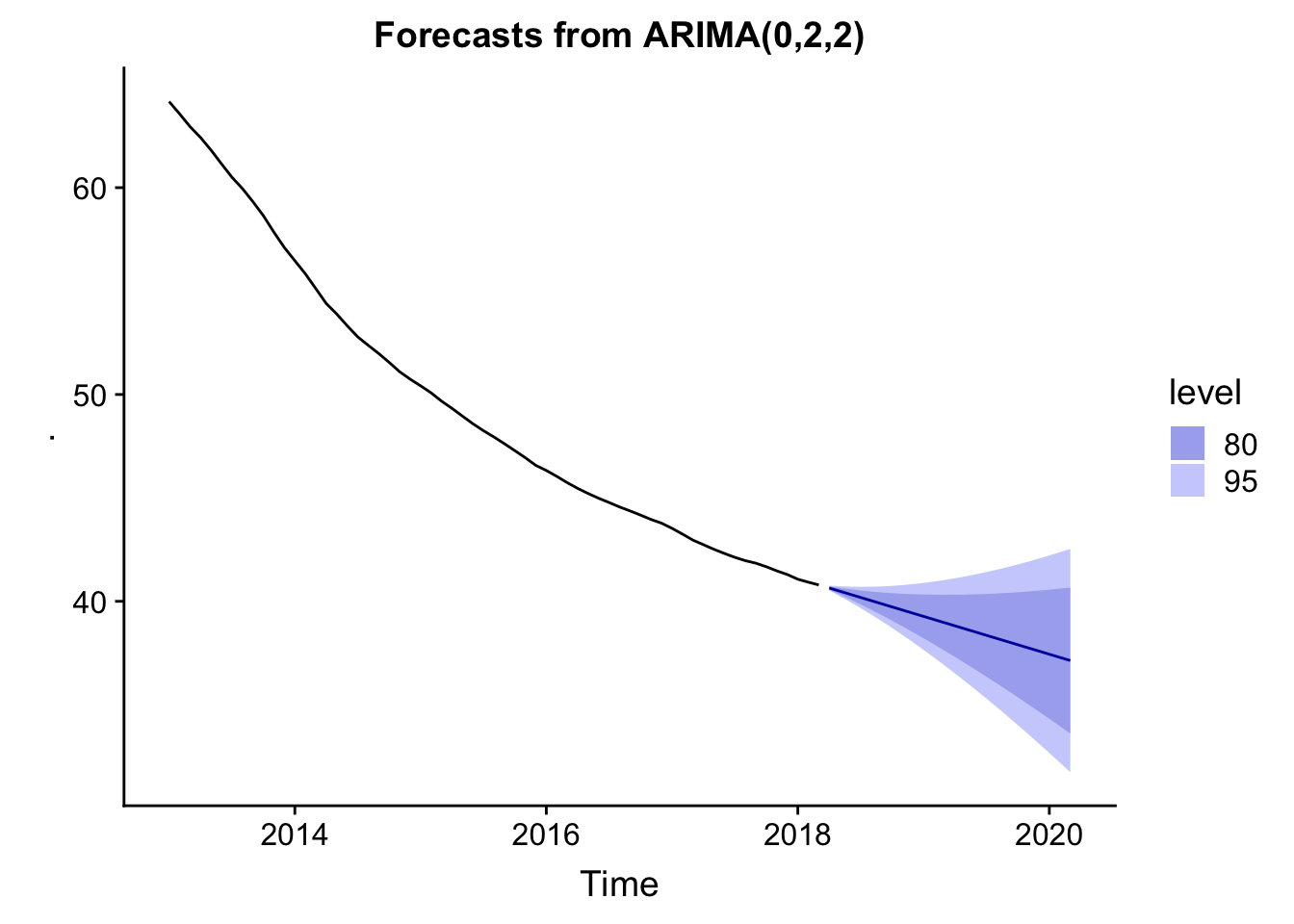
# Tabla de datos del forecast
fc_arima## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## Apr 2018 40.64287 40.56759 40.71814 40.52775 40.75799
## May 2018 40.49043 40.33337 40.64749 40.25023 40.73063
## Jun 2018 40.33800 40.09480 40.58119 39.96606 40.70994
## Jul 2018 40.18556 39.84840 40.52272 39.66992 40.70120
## Aug 2018 40.03313 39.59400 40.47226 39.36153 40.70472
## Sep 2018 39.88069 39.33187 40.42951 39.04135 40.72004
## Oct 2018 39.72826 39.06241 40.39411 38.70993 40.74659
## Nov 2018 39.57582 38.78597 40.36567 38.36785 40.78380
## Dec 2018 39.42339 38.50290 40.34388 38.01562 40.83116
## Jan 2019 39.27095 38.21347 40.32844 37.65368 40.88823
## Feb 2019 39.11852 37.91797 40.31907 37.28244 40.95460
## Mar 2019 38.96609 37.61663 40.31554 36.90227 41.02990
## Apr 2019 38.81365 37.30966 40.31764 36.51349 41.11381
## May 2019 38.66122 36.99725 40.32518 36.11641 41.20603
## Jun 2019 38.50878 36.67959 40.33797 35.71127 41.30629
## Jul 2019 38.35635 36.35682 40.35587 35.29834 41.41435
## Aug 2019 38.20391 36.02910 40.37872 34.87783 41.52999
## Sep 2019 38.05148 35.69657 40.40639 34.44995 41.65301
## Oct 2019 37.89904 35.35933 40.43876 34.01489 41.78320
## Nov 2019 37.74661 35.01752 40.47570 33.57282 41.92040
## Dec 2019 37.59417 34.67123 40.51712 33.12392 42.06443
## Jan 2020 37.44174 34.32057 40.56291 32.66832 42.21516
## Feb 2020 37.28930 33.96563 40.61298 32.20618 42.37243
## Mar 2020 37.13687 33.60650 40.66724 31.73764 42.53610Conclusión
Para marzo de 2020, el forecast mediante el método Holt predice un % de mercado regulado con un intervalo de confianza inferior del 80% entre del 38.15% y 35.30%.
El método ARIMA, por su parte lo sitúa entre el 37.13% y el 33.60%.
Ambos son muy parecidos, y como primera aproximación nos da un recorrido bastante plausible del futuro cercado. Estaré atento a la CNMC en su publicación del primer trimestre de 2020.