En anteriores entradas he modelizado la demanda peninsular de REE (concretamente la previsión de dicha demanda) con diferentes aproximaciones y técnicas. Básicamente, he tratado de predecir el consumo diario con bastante éxito a través de random forest, correlacionando los datos de temperatura del aeropuerto de Madrid a nivel diario y creando variables nuevas que identificaban el tipo de días (festivo o laboral), el día de la semana, el mes o el quarter.
A continuación, me he atrevido a realizar el mismo modelo pero con una granularidad horaria, al poder adquirir de forma gratuita los datos de temperatura horarios de la estación meteorológica del aeropuerto en cuestión. El R2 del modelo, o varianza explicada por el mismo, cayó estrepitosamente, poniendo de manifiesto que este tipo de predicción tienen un plus de dificultad respecto a la predicción horaria.
Aproximación por series temporales
En esta entrada, trataré con series temporales (en adelante time-series), que son objetos cuya naturaleza implican que puede existir una autocorrelación entre los valores (de consumo en este caso) de una serie dada. Parece obvio que en el sector eléctrico, el efecto curva o apalancamiento o apuntamiento dé lugar a trabajar con time-series, dado que efectivamente existen unos patrones repetitivos de consumo a lo largo del tiempo.
Datos de partida
Recuperando el dataset de la previsión de datos de REE, tengo:
Para la modelización, utilizaré una aproximación univariada, es decir, únicamente con la variable de la propia previsión de demanda. Por tanto, no hará falta generar variables nuevas que indiquen días festivos, de la semana, del mes u otros.
Una obviedad que merece la pena resaltar es que los datos presentan múltiples estacinoalidades (como cualquier curva de consumo), concretamente:
- Estacionalidad horaria: en frecuencias de 24 horas.
- Estacionalidad semanal: en frecuencias de 7 días (o 168 horas).
La mayoría de los modelos de time-series no permiten múltiples estacionalidades, y en general, no trabajan con datos horarias, sino diarios o de frecuencias menores. Esto supone un grave problema, ya que no tendría demasiado sentido aplicar un modelo ARIMA como hice en el forecast del % cuota de mercado regulado vs mercado liberalizado, cuya frecuencia era mensual.
Sin embargo, se dispone de una opción que podría arrojar un resultado aceptable: el modelo TBATS.
Modelo TBATS
Este modelo, introducido por De Livera, Hyndman & Snyder (2011, JASA), permite modelizar múltiples estacionalidades, aunque por contra, no permite añadir regresores o variables independientes como la temperatura, por ejemplo. Como curiosidad, el acrónimo del modelo viene de:
- T (Trigonometric regressors): regresores trigonométricos para múltiples estacionalidades.
- B (Box-Cox transformations): transformación de Box-Cox, para corregir el defecto de normalidad en los datos.
- A (ARMA errors): modelización de los errores del ARIMA.
- T (trend): tendencia.
- S (seasonality): estacionalidad.
Dado que el TBATS es computacionalmente lento de calcular, realizaré la modelización sobre los datos correspondientes al 1 de junio de 2018 en adelante, y este será el set de entrenamiento. Me reservaré los últimos 10 días para realizar la predicción (este será el set de testeo).
library(xts)
library(forecast)
# Transformo el dataset en una serie temporal
prevision_demanda_ts <- prevision_demanda_horaria %>%
filter(datetime >= "2018-06-01") %>%
select(prevision_demanda) %>%
ts()
# Set de entrenamiento 4 meses aprox.
trainset <- subset(prevision_demanda_ts, end=length(prevision_demanda_ts)-241)
# Set de testeo de 10 días
testset <- subset(prevision_demanda_ts, start=length(prevision_demanda_ts)-240)
# Entrenamiento del modelo TBATS
fit_trainset_tbats <- tbats(trainset, seasonal.periods = c(24, 168))
# Grafico la descomposición de la serie
plot(fit_trainset_tbats)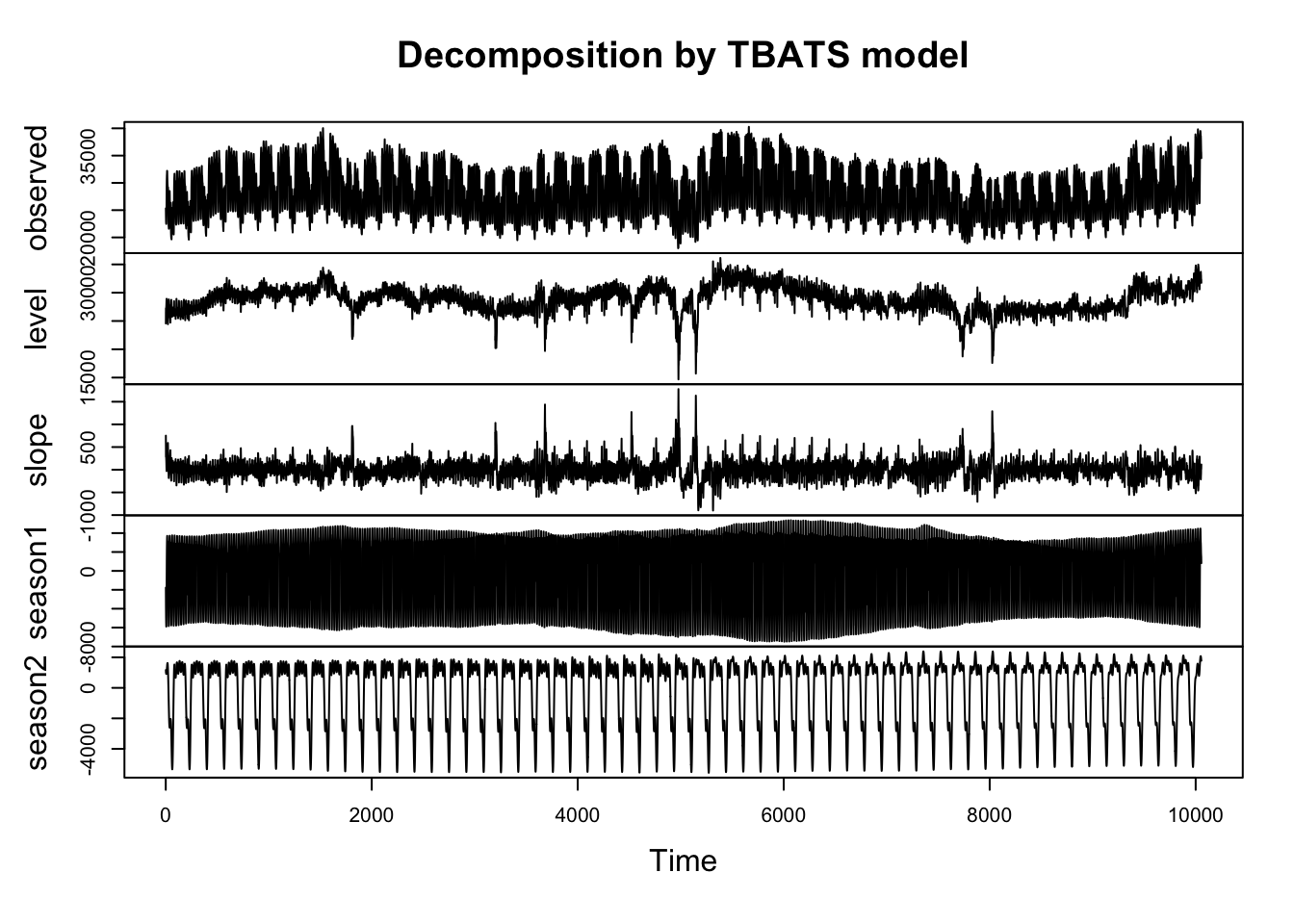
# Datos del modelo
fit_trainset_tbats## TBATS(1, {0,0}, 0.831, {<24,7>, <168,6>})
##
## Call: tbats(y = trainset, seasonal.periods = c(24, 168))
##
## Parameters
## Alpha: 1.426551
## Beta: -0.2330395
## Damping Parameter: 0.831458
## Gamma-1 Values: 0.01471845 0.004716359
## Gamma-2 Values: 0.008688517 -0.00408338
##
## Seed States:
## [,1]
## [1,] 29127.825270
## [2,] 5.449883
## [3,] -2467.450352
## [4,] 1285.492527
## [5,] -155.725662
## [6,] -362.217476
## [7,] -121.219418
## [8,] 9.648324
## [9,] 46.560268
## [10,] -3331.501136
## [11,] -1779.779363
## [12,] -245.538094
## [13,] -21.105890
## [14,] -39.894466
## [15,] 102.230859
## [16,] 41.831230
## [17,] 971.055483
## [18,] 871.662167
## [19,] -566.646483
## [20,] 419.652866
## [21,] -560.153496
## [22,] 33.506233
## [23,] -2083.491535
## [24,] 1041.996178
## [25,] -52.565564
## [26,] 128.587295
## [27,] 280.831701
## [28,] -681.190654
##
## Sigma: 474.5424
## AIC: 216660# Grafico residuos del modelo
checkresiduals(fit_trainset_tbats)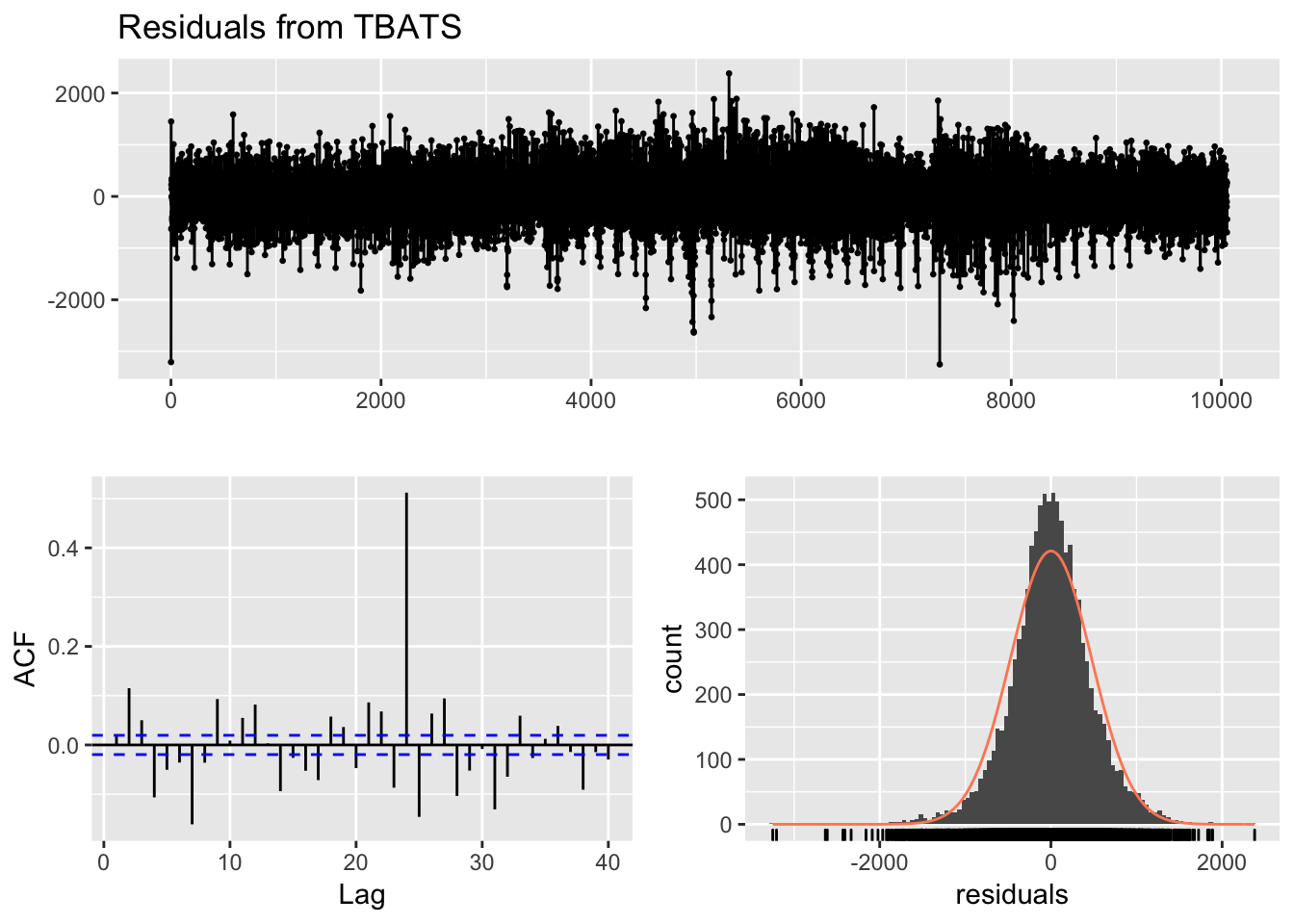
##
## Ljung-Box test
##
## data: Residuals from TBATS
## Q* = 4699.7, df = 3, p-value < 2.2e-16
##
## Model df: 35. Total lags used: 38El gráfico de descomposición del time-series muestra las dos estacionalidades, horaria (muy comprimida y poco visible ciertamente) y la semanal, mucho más obvia visualmente.
El gráfico ACF o de autocorrelación muestra un pico significativo en el valor 24 (obvio, es una de las estacionalidades) y también son relevantes picos en las horas 3, 5 y 7, posiblemente dado por el efecto curva del consumo.
Por último, el histograma de residuos o errores muestra una distribución normal, y cuya media es 0, lo que parece indicar que el modelo se deja poca información para explicar la variabilidad.
Predicción de 10 días de demanda horaria
Realizaré ahora la predicción sobre unos datos ciegos al entrenamiento, de 10 días:
# Realizo predicción sobre los 10 días de testeo
demanda_forecast <- forecast(fit_trainset_tbats, h=240)
# Grafico resultado
autoplot(demanda_forecast) + autolayer(testset)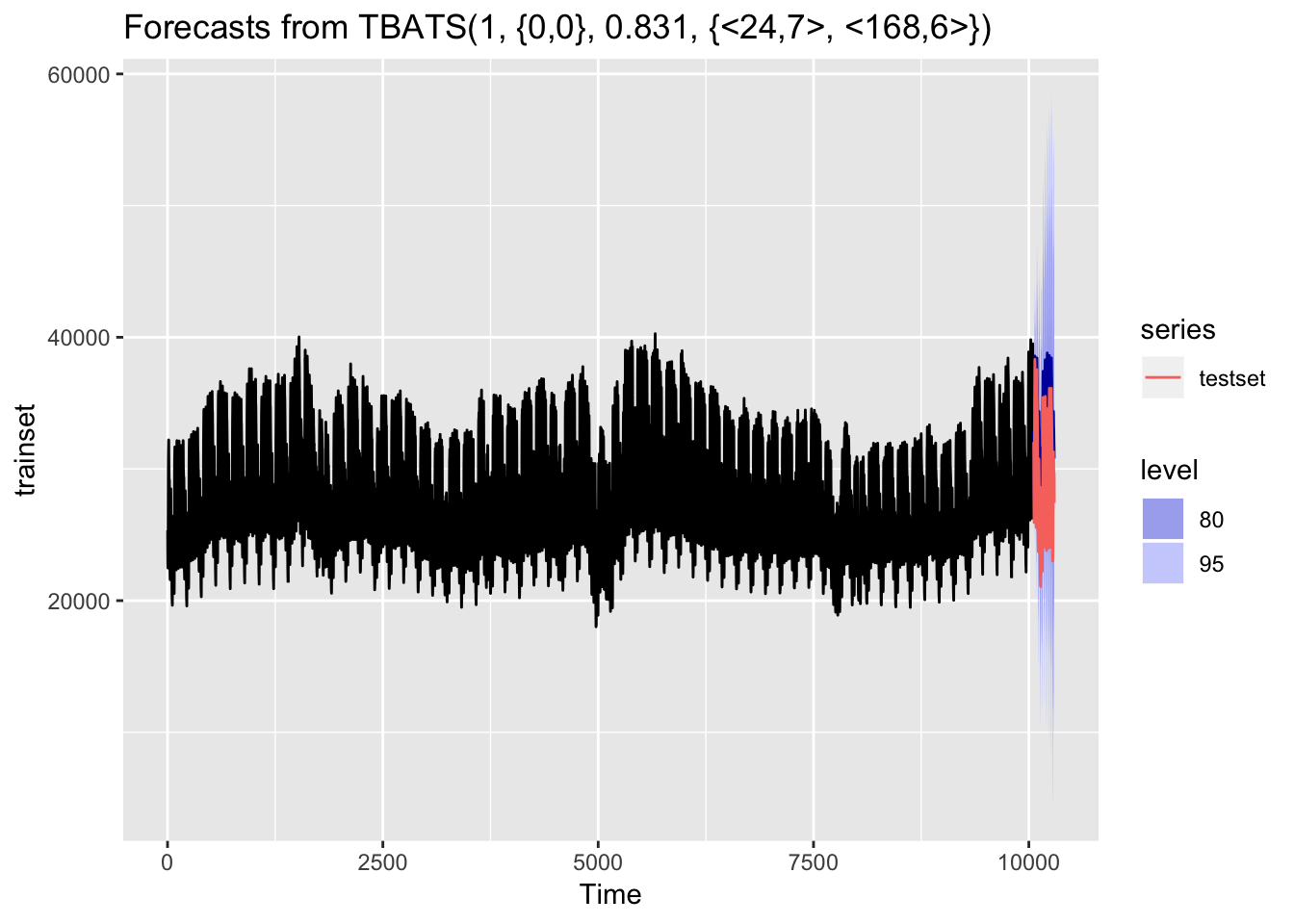
# Medidas del error sobre el set de testeo
accuracy(demanda_forecast, testset)## ME RMSE MAE MPE MAPE
## Training set 1.135942 474.5424 355.3582 -0.0268103 1.269848
## Test set -2737.352974 2951.7225 2744.0073 -9.6010430 9.619023
## MASE ACF1 Theil's U
## Training set 0.3449914 0.01736922 NA
## Test set 2.6639569 0.93412796 2.636065Los resultados arrojan un error medio absoluto (MAE) de 355 MWh (o 1.26%) en el set de entrenamiento y de 2744 MWh (o 9.61%) en el set de testeo. No está mal para empezar con una aproximación simple, simplemente escogiendo el modelo que tiene sentido escoger dada la naturaleza de nuestros datos.
Podría iterar sobre el set de entramiento ideal, (más corto, más largo…) y lógicamente acotar el forecast a las siguientes 24 horas, que es para cuando el operador realizaría la compra de energía en el mercado mayorista. Aquí es donde realmente empezaría el trabajo del analista.