Si bien en la anterior entrada realicé una aproximación para la predicción del consumo eléctrico a través de time-series, en esta utilizaré uno de los modelos más conocidos de forecasting: el ARIMA.
Los modelos ARIMA funcionan bien cuando se disponen de series temporales largas (más de 40 puntos al menos) y el patrón de comportamiento es estable o consistente durante el tiempo. Requieren que la serie sea estacionaria, lo cual quiere decir que no deben tener una tendencia ni tampoco una variabilidad entre picos elevada. Aquí se explica muy bien el concepto.
¿Pero qué significa ARIMA?
Es un modelo con 3 términos diferenciadss:
- AR: término autoregresivo. Establece la relación entre un valor determinado y otro anterior (laggeado).
- I: integrado. Se refiere a la capacidad de diferenciar la serie para eliminar la tendencia y la variabilidad creciente o decreciente.
- MA: término moving average. Representa el error del modelo como cobinación de términos de error anteriores.
Otra ventaja de los ARIMA es que permiten adaptarse a cualquier frecuencia utilizando términos de Fourier, y además, utilizar variables externas que ayuden a mejorar el modelo (festivos, temperatura, etc.).
Datos de partida
Recuperando el dataset de la previsión de datos de REE, tengo en principio tres tablas:
- Serie temporal de previsión de demanda de ESIOS.
- Serie temporal indicando los días festivos.
- Serie temporal de temperatura horaria de Madrid-Barajas.
library(lubridate)
library(dplyr)
library(ggplot2)
library(riem)
library(weathermetrics)
library(readr)
library(tidyr)
library(xts)
library(forecast)
library(anomalize)
# Leo archivo de previsión de demanda
prevision_demanda <- read_csv2("/Users/pherreraariza/Documents/energychisquared_v2/post_inputs/8_post/previsionDemanda.csv") %>% select(datetime, value)
# Leo archivo de temperatura de Barajas
temperatura <- read_csv2("/Users/pherreraariza/Documents/energychisquared_v2/post_inputs/8_post/barajas.csv")
# Leo archivo de festivos nacionales
festivos <- read_csv2("/Users/pherreraariza/Documents/energychisquared_v2/post_inputs/8_post/festivos.csv", col_types = "cc", col_names = TRUE) %>% mutate(fecha = as.Date(fecha, format = "%d-%m-%Y"), tipo = 1)Puesto que el entrenamiento del modelo de una serie muy larga puede ser computacionalmente costoso, filtraré los datos para contemplar sólo desde el primer lunes de agosto hasta el domingo 21 de octubre (¡antes del cambio de hora!).
Sobre este set de datos, es necesario transformar la serie temporal indicando que existen dos estacionalidades:
- Estacionalidad horaria: donde la frecuencia es igual a 24.
- Estacionalidad semanal: donde la frecuencia es igual a 24 · 7 = 168.
Realizaré un análisis de autocorrelación total y parcial, así como una descomposición de la serie temporal de la demanda eléctrica, para ver algunos insights:
# Transformo a time series y fijo frecuencia
prevision_demanda_ts <- prevision_demanda %>% filter(as.Date(datetime) >= "2018-08-06 00:00:00",
as.Date(datetime) <= "2018-10-21 00:00:00") %>%
select(value) %>%
msts(c(24,168))
# Análisis de autocorrelación y autocorrelación parcial
Acf(prevision_demanda_ts)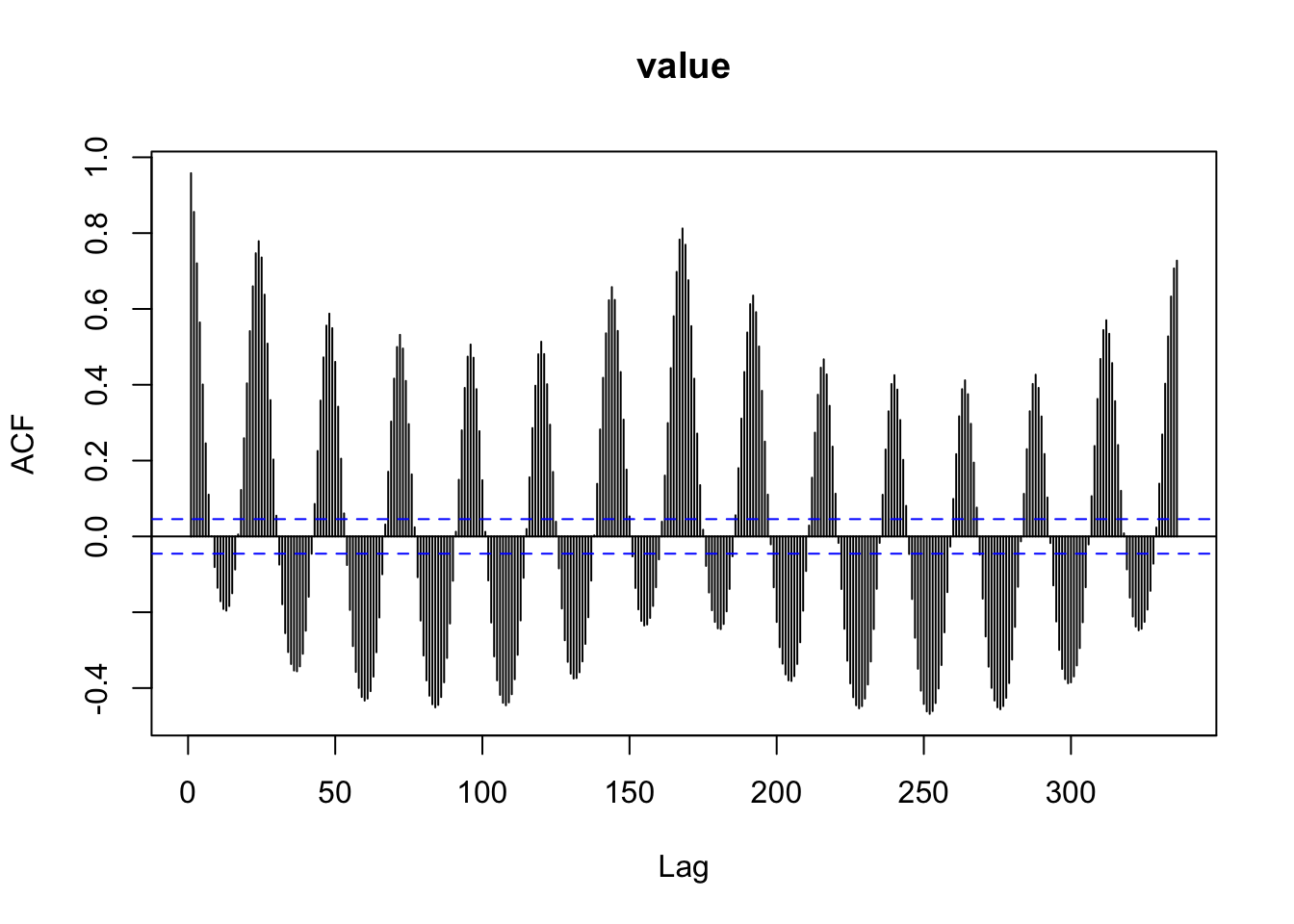
Pacf(prevision_demanda_ts)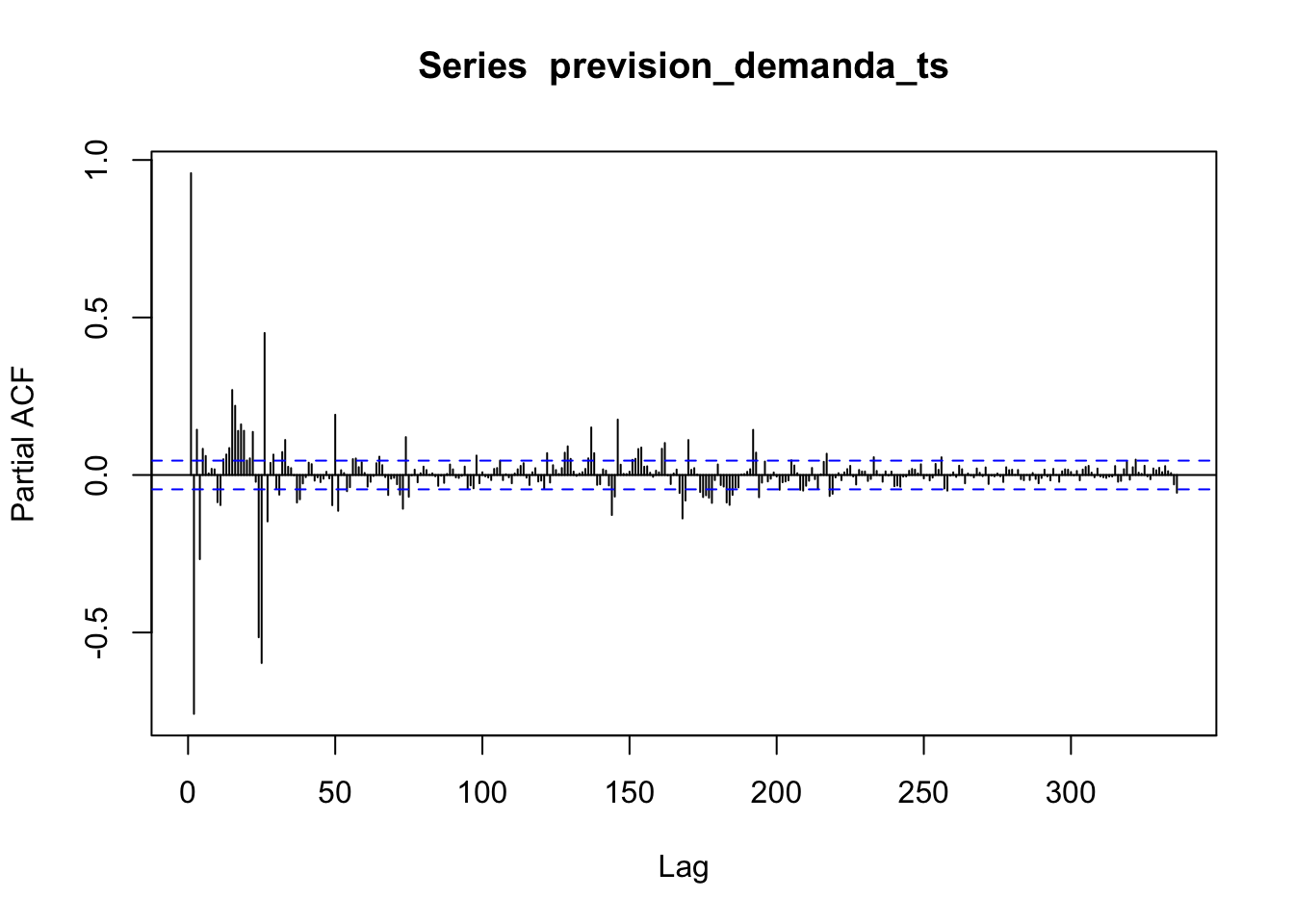
El primer gráfico indica claramente la fuerte autocorrelación existente entre los valores laggeados de la serie, y destaca la estacionalidad. El segundo gráfico es más difícil de interpretar, pero debido a la forma de tail-off, donde los valores cada vez se van haciendo más pequeños, parece típico de los modelos ARIMA.
A continuación se representa la descomposición de la serie temporal:
# Múltiple estacionalidad
mstl(prevision_demanda_ts, lambda='auto') %>% autoplot(facet=TRUE)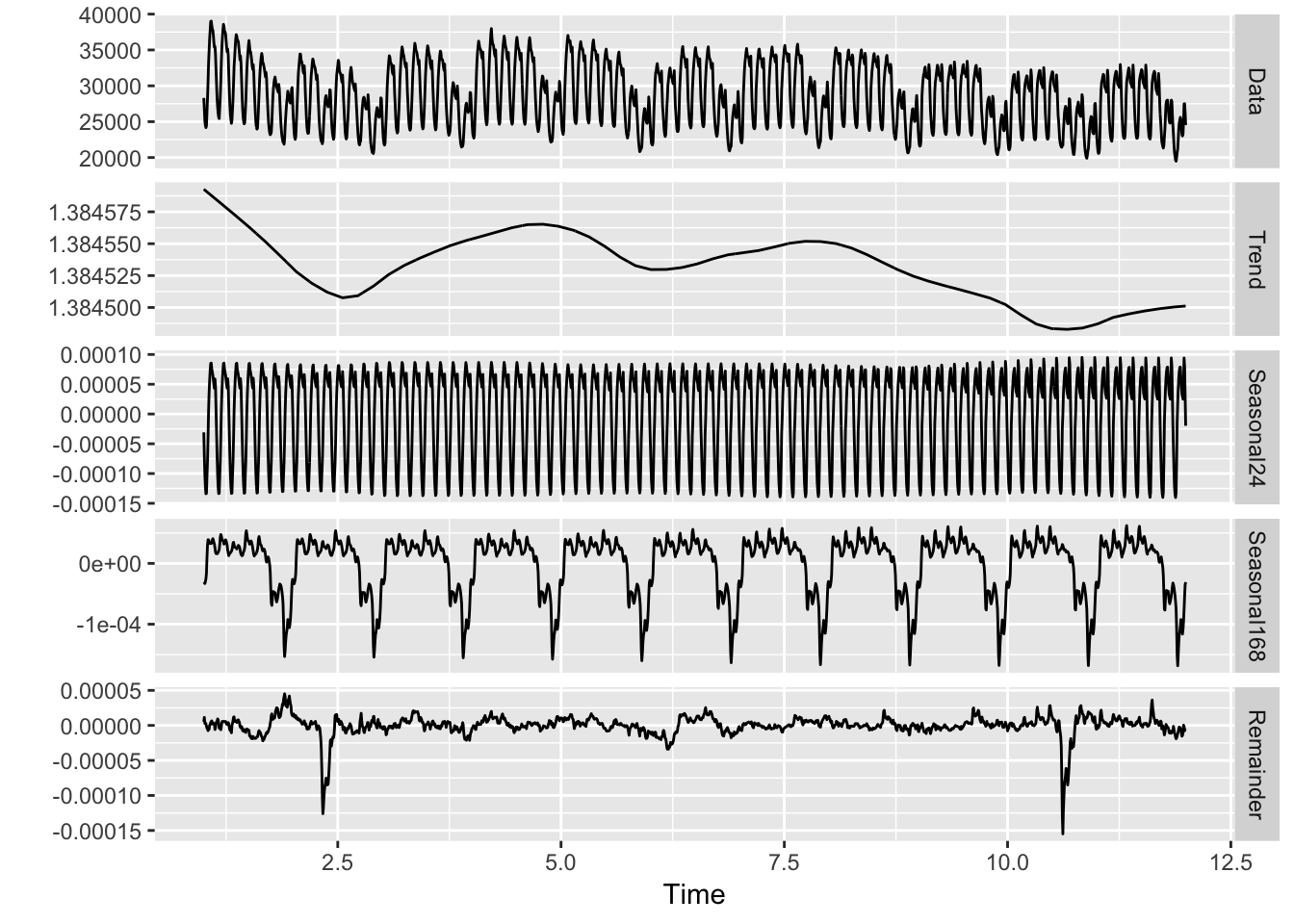
Como puede verse, los datos originales son descompuestos en 4 series:
- Trend: o tendencia. Claramente la tendencia general de los datos varía suavemente, decreciendo en las primeras semanas de agosto para después mantenerse hasta casi las últimas, donde de nuevo decae (mediados de octubre).
- Seasonal24: es la primera estacionalidad fijada, la del ciclo horario.
- Seasonal168: es la segunda estacionalidad, la semanal.
- Remainder: es el resto o residuo de la serie, donde trabajará el moddelo. Existen dos puntos de la serie a principios y finales del periodo, que será difícil que el modelo pueda fijar bien.
Entrenamiento del modelo ARIMA univariado con series de Fourier
En la entrada anterior, expliqué que el modelo TBATS era muy apropiado para abordar series temporales con múltiple estacionalidad, pero ARIMA también puede contemplar una solución a este problema: aplicando las series de Fourier.
Estos términos, que no son otra cosa que series en pares de seno y coseno ajustados a una frecuencia concreta, pueden simular cualquier estacionalidad múltiple (aunque hay que ajustarlos), por lo que estableceré a un K(10, 10) la serie y ajustaré el modelo.
# Defino sets de entrenamiento y test
trainset <- subset(prevision_demanda_ts, end=length(prevision_demanda_ts)-(24*7))
testset <- subset(prevision_demanda_ts, start=length(prevision_demanda_ts)-(24*7)+1)
# Modelo ARIMA con series de fourier
fit_fourier <- auto.arima(trainset, seasonal = FALSE, xreg = fourier(trainset, K=c(10,10)))
forecast_fourier <- forecast(fit_fourier, xreg = fourier(testset, K=c(10,10), 24*7), 24*7)
# Grafico resultado
autoplot(forecast_fourier) + autolayer(testset)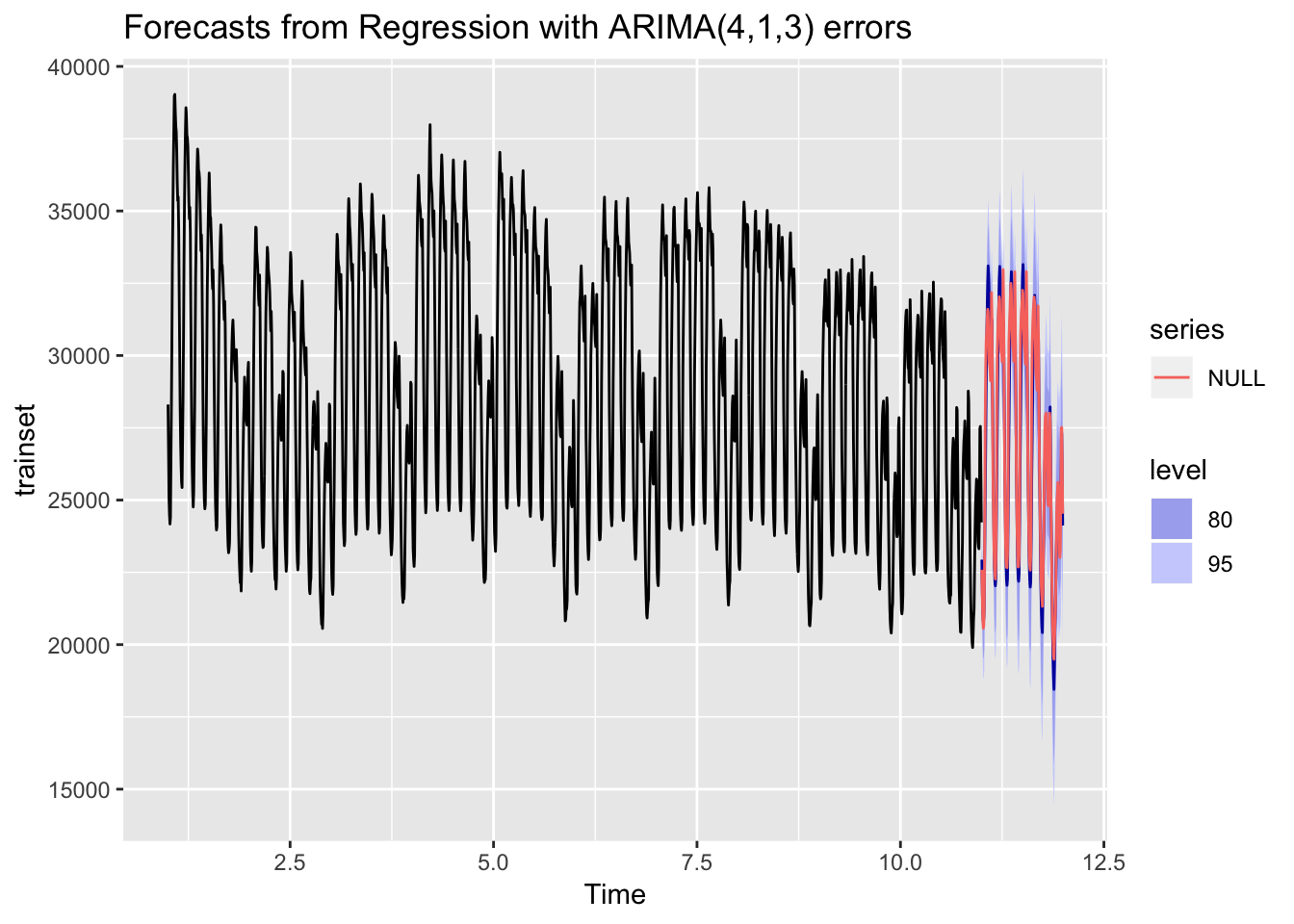
checkresiduals(fit_fourier)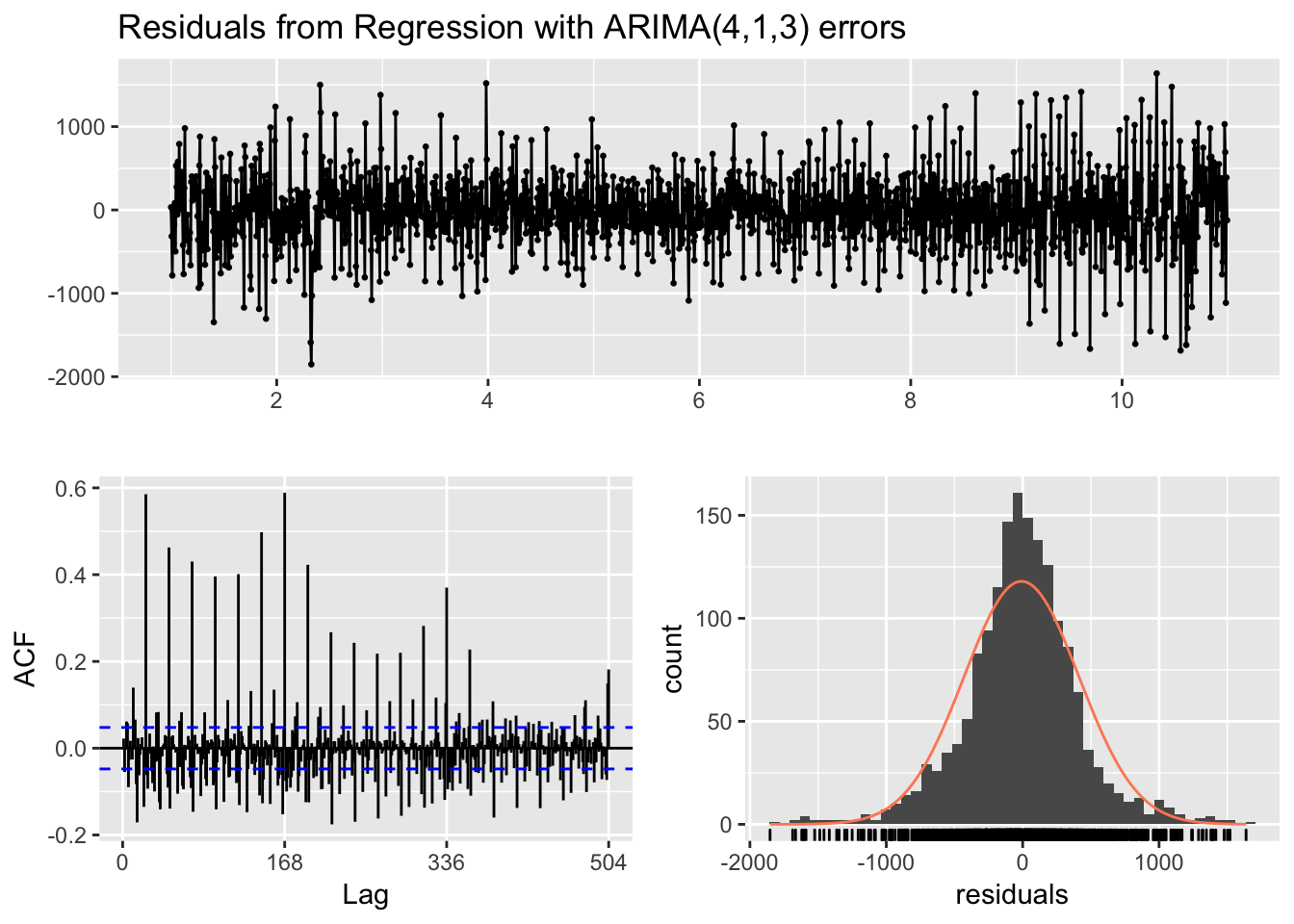
##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(4,1,3) errors
## Q* = 6352.5, df = 291, p-value < 2.2e-16
##
## Model df: 45. Total lags used: 336# Calculo error MAPE
MAPE_ARIMA_univariado <- accuracy(forecast_fourier, testset)Parece que el resultado no es del todo malo. De hecho sorprende el error MAPE que sea tan bajo, comparándolo con el modelo TBATS.
Entrenamiento del modelo ARIMA con festivos incluidos con series de Fourier
Una cualidad de diferencia al TBATS del ARIMA, es que el segundo puede modelizar con regresores o variables externas para aginar el resultado. En este primer intento, incluiré con 1 y 0, si un día en concreto es festivo o no, así como si es fin de semana, dado que la demanda decae fuertemente en dichos días.
# Genero la tabla con todas la variables
prevision_demanda_cov <- prevision_demanda %>% left_join(temperatura, by = c("datetime" = "hour")) %>%
mutate(datetime = as.Date(datetime),
fechadummy = as.Date(datetime)) %>%
left_join(festivos, by = c("fechadummy" = "fecha")) %>%
mutate(weekday = as.factor(wday(fechadummy)),
tipo = if_else(is.na(tipo) & weekday %in% c(2,3,4,5,6), 0, 1)) %>%
select(-fechadummy, -weekday)
# Transformo a time series y fijo frecuencia
prevision_demanda_cov_ts <- prevision_demanda_cov %>% filter(as.Date(datetime) >= "2018-08-06 00:00:00",
as.Date(datetime) <= "2018-10-21 00:00:00") %>%
select(value, tipo, temperature) %>%
msts(c(24,168))Una vez creada la serie temporal, entreno el modelo con las series de Fourier y los festivos:
# Defino sets de entrenamiento y test para demanda
trainset_cov <- subset(prevision_demanda_cov_ts[, "value"], end = length(prevision_demanda_cov_ts[, "value"])-(24*7))
testset_cov <- subset(prevision_demanda_cov_ts[, "value"], start = length(prevision_demanda_cov_ts[, "value"])-(24*7)+1)
# Defino sets de entrenamiento y test para series de fourier
fourier_xreg_train <- fourier(trainset_cov, K=c(10,10))
fourier_xref_test <- fourier(testset_cov, K=c(10,10), 24*7)
# Defino sets de entrenamiento y test para festivos
tipo_festivos <- prevision_demanda_cov_ts[, "tipo"]
tipo_festivo_train <- subset(tipo_festivos, end = length(tipo_festivos)-(24*7))
tipo_festivo_test <- subset(tipo_festivos, start = length(tipo_festivos)-(24*7)+1)
# Ajusto el modelo ARIMA con series de fourier y covariables
fit_regresores <- auto.arima(trainset_cov, seasonal = FALSE, xreg = cbind(fourier_xreg_train, tipo_festivo_train))
forecast_regresores <- forecast(fit_regresores, xreg = cbind(fourier_xref_test, tipo_festivo_test), 24*7)
# Grafico resultado
autoplot(forecast_regresores) + autolayer(testset_cov)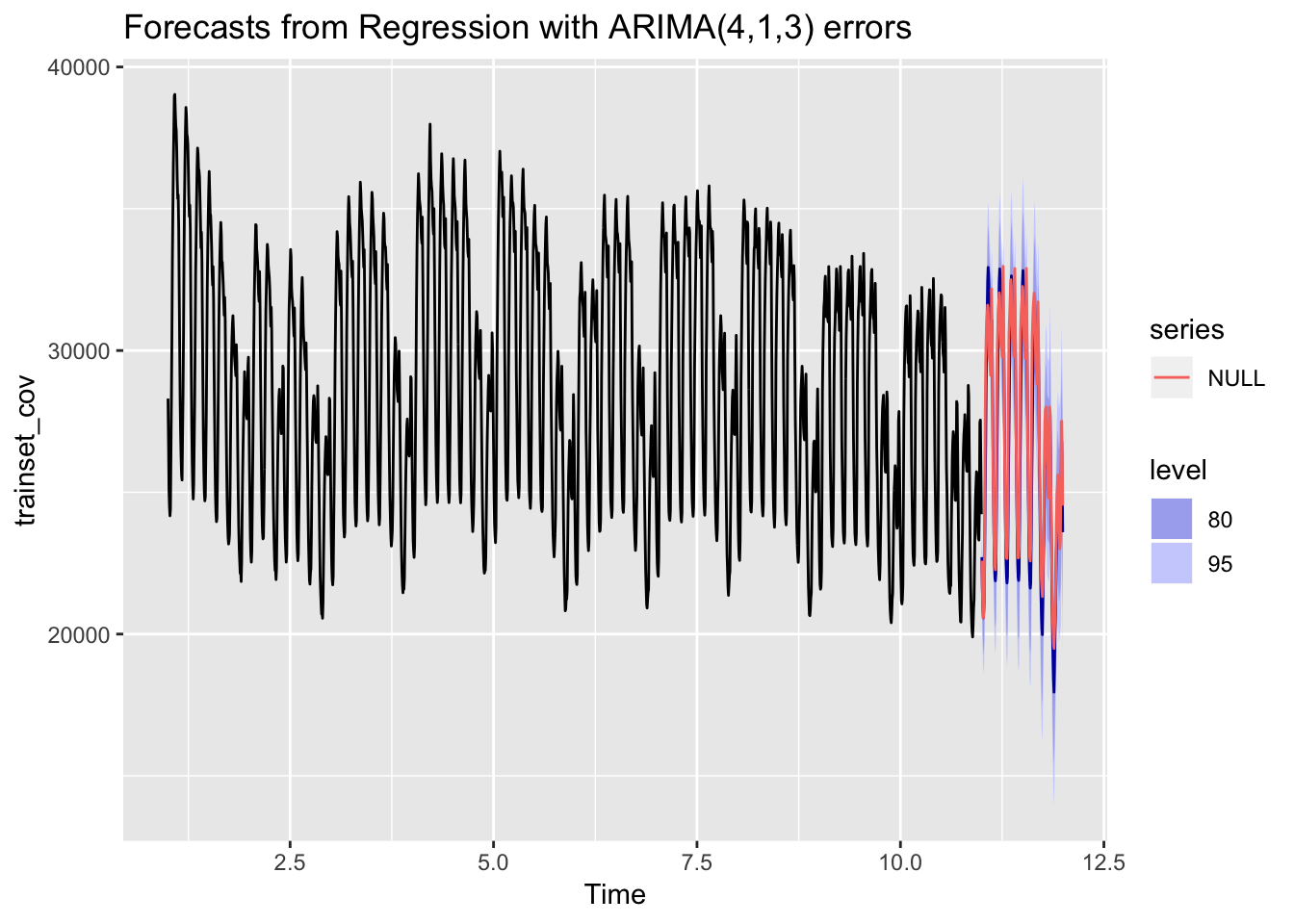
checkresiduals(fit_regresores)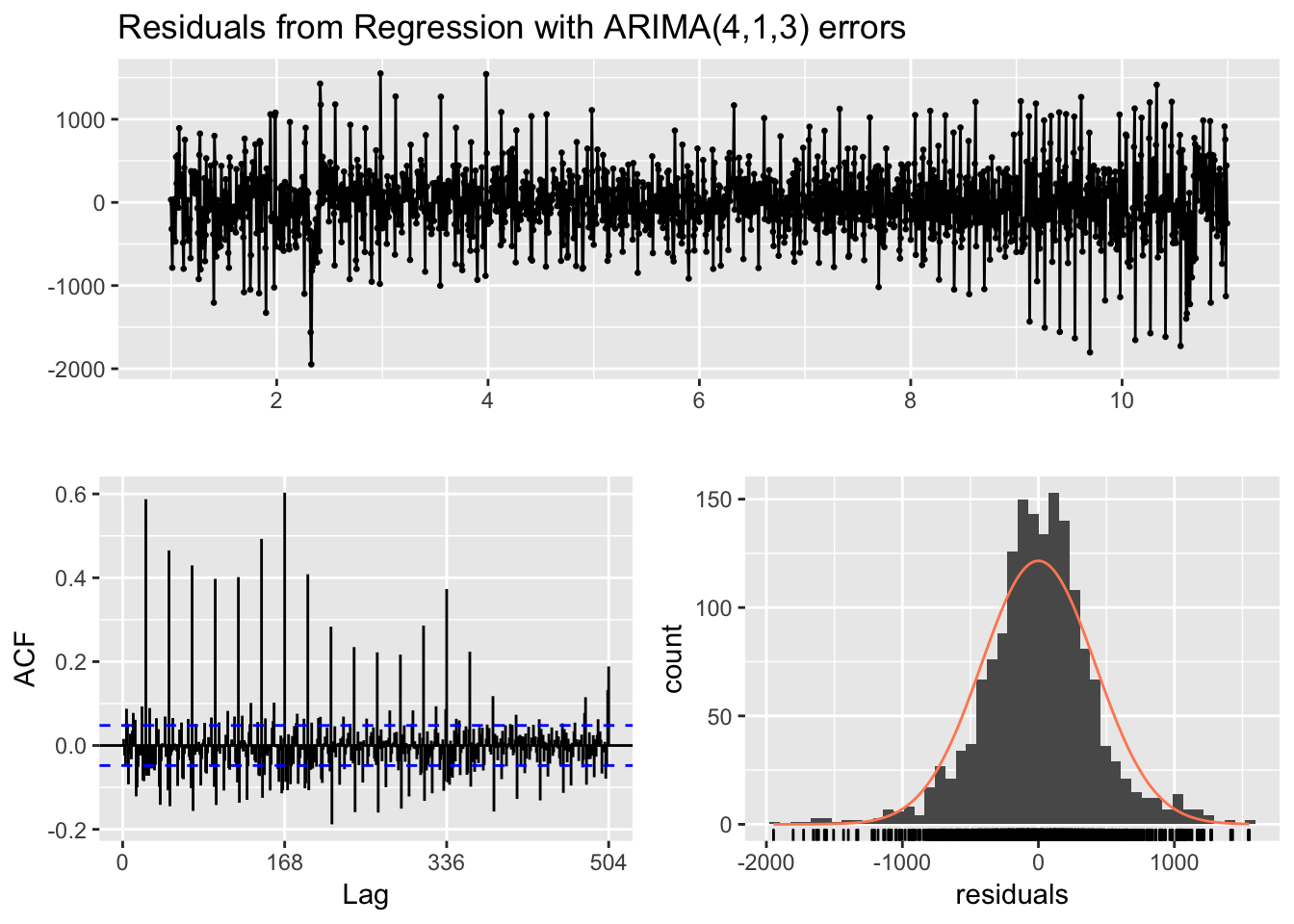
##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(4,1,3) errors
## Q* = 6150.5, df = 289, p-value < 2.2e-16
##
## Model df: 47. Total lags used: 336# Calculo error MAPE
MAPE_ARIMA_festivos <- accuracy(forecast_regresores, testset_cov)El error MAPE sorprendentemente es más alto que con el modelo anterior.
Entrenamiento del modelo ARIMA con festivos y temperatura incluidos con series de Fourier
Por último, añadiré la temperatura como variable externa para ver si mejora el modelo. Como lo habitual es que los valores horarios de temperatura contengan huecos, lo más fácil es interpolar para resolver esta cuestión:
# Añado temperatura como covariable
temperatura_train <- subset(prevision_demanda_cov_ts[, "temperature"], end = length(prevision_demanda_cov_ts[, "temperature"])-(24*7))
temperatura_test <- subset(prevision_demanda_cov_ts[, "temperature"], start = length(prevision_demanda_cov_ts[, "temperature"])-(24*7)+1)
# Interpolo huecos
temperatura_train_filled <- na.interp(temperatura_train)
temperatura_test_filled <- na.interp(temperatura_test)
# Grafico interpolación
autoplot(temperatura_train_filled, series="Interpolated") +
autolayer(temperatura_train, series="Original") +
scale_colour_manual(values=c(`Interpolated`="red",`Original`="gray"))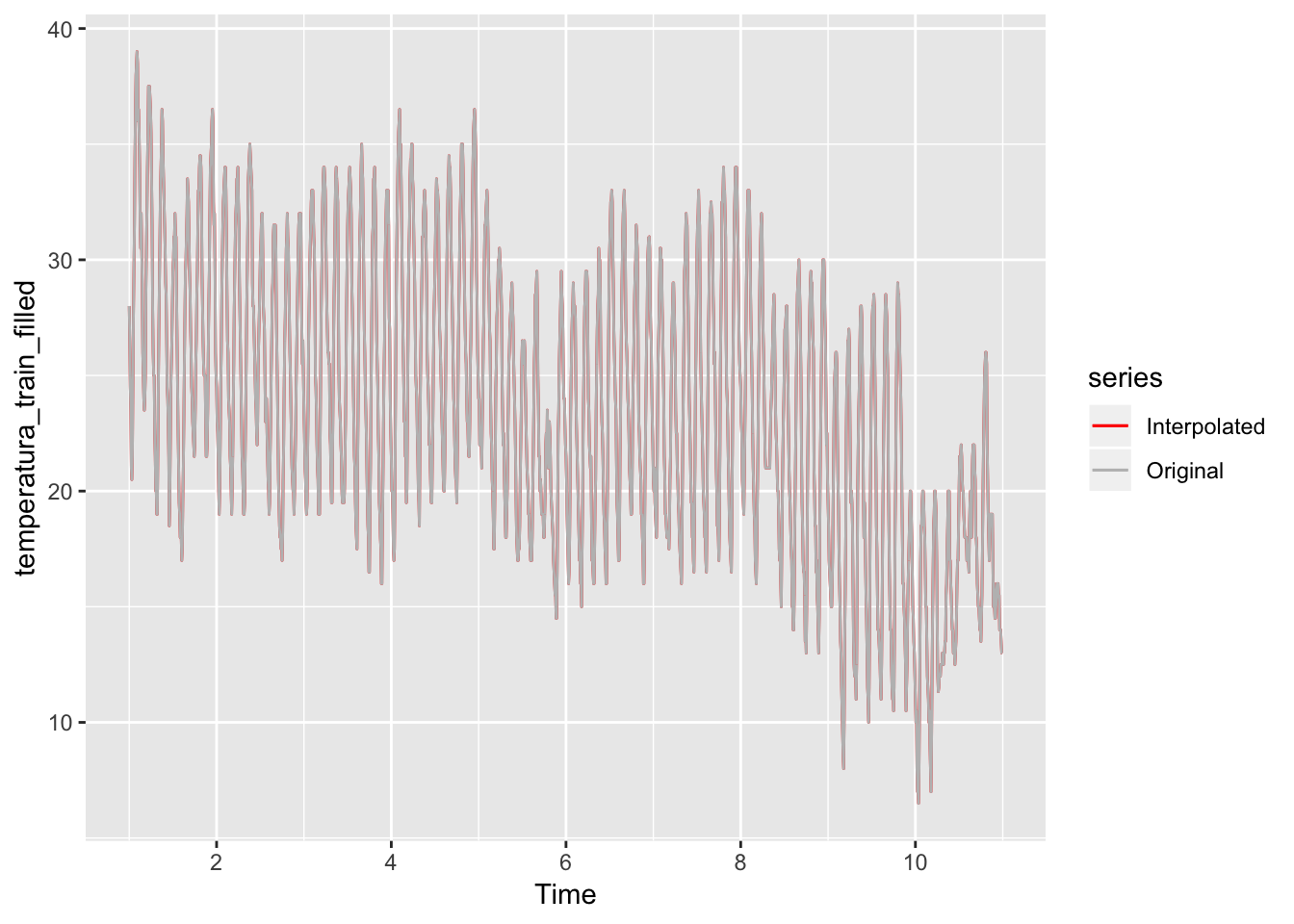
A continuación entreno el modelo:
# Ajusto modelo ARIMA con todas las covariables
fit_regresores_total <- auto.arima(trainset_cov, seasonal = FALSE, xreg = cbind(fourier_xreg_train, tipo_festivo_train, temperatura_train_filled))
forecast_regresores_total <- forecast(fit_regresores_total, xreg = cbind(fourier_xref_test, tipo_festivo_test, temperatura_test_filled), 24*7)
# Grafico resultado
autoplot(forecast_regresores_total) + autolayer(testset_cov)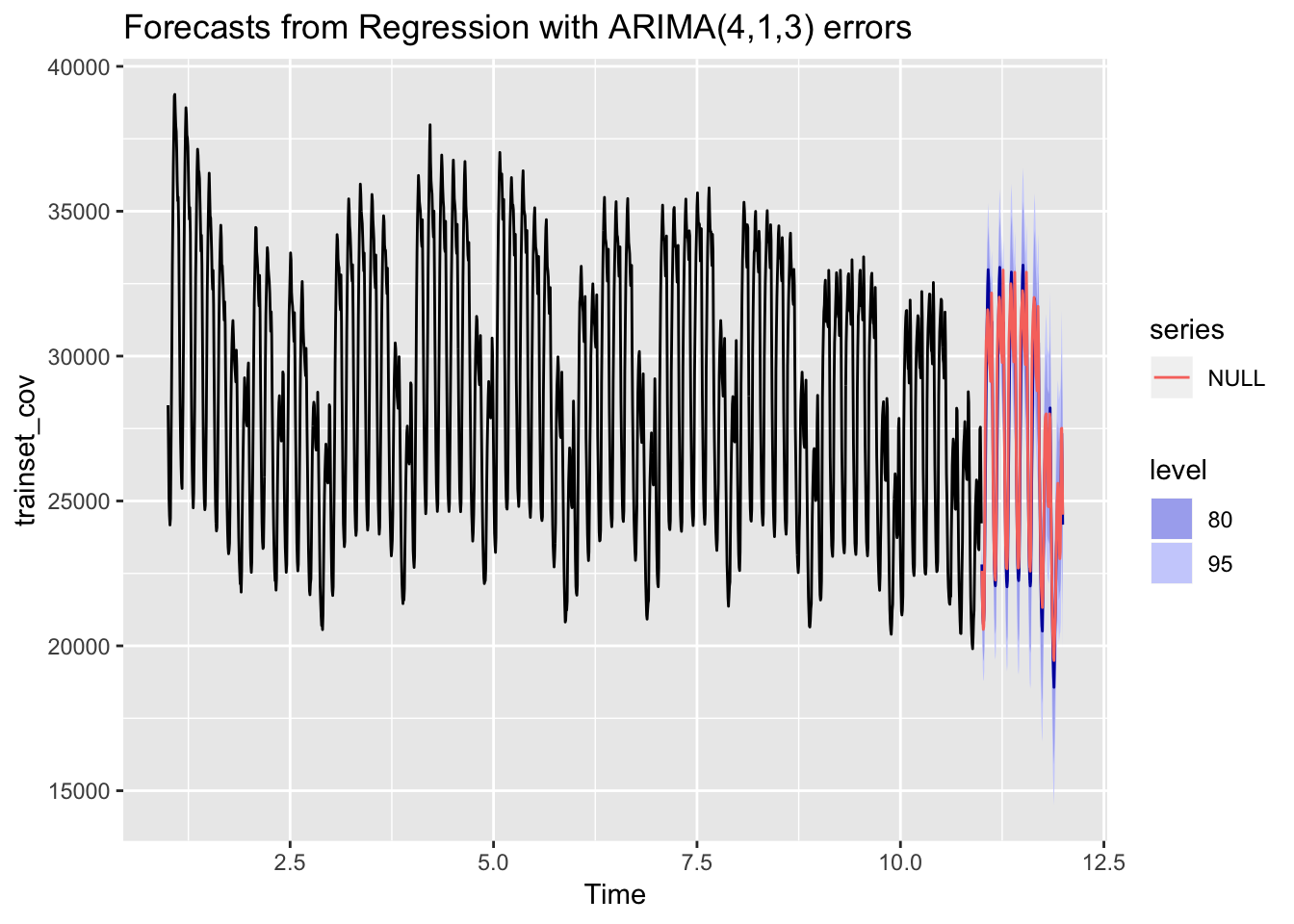
checkresiduals(fit_regresores_total)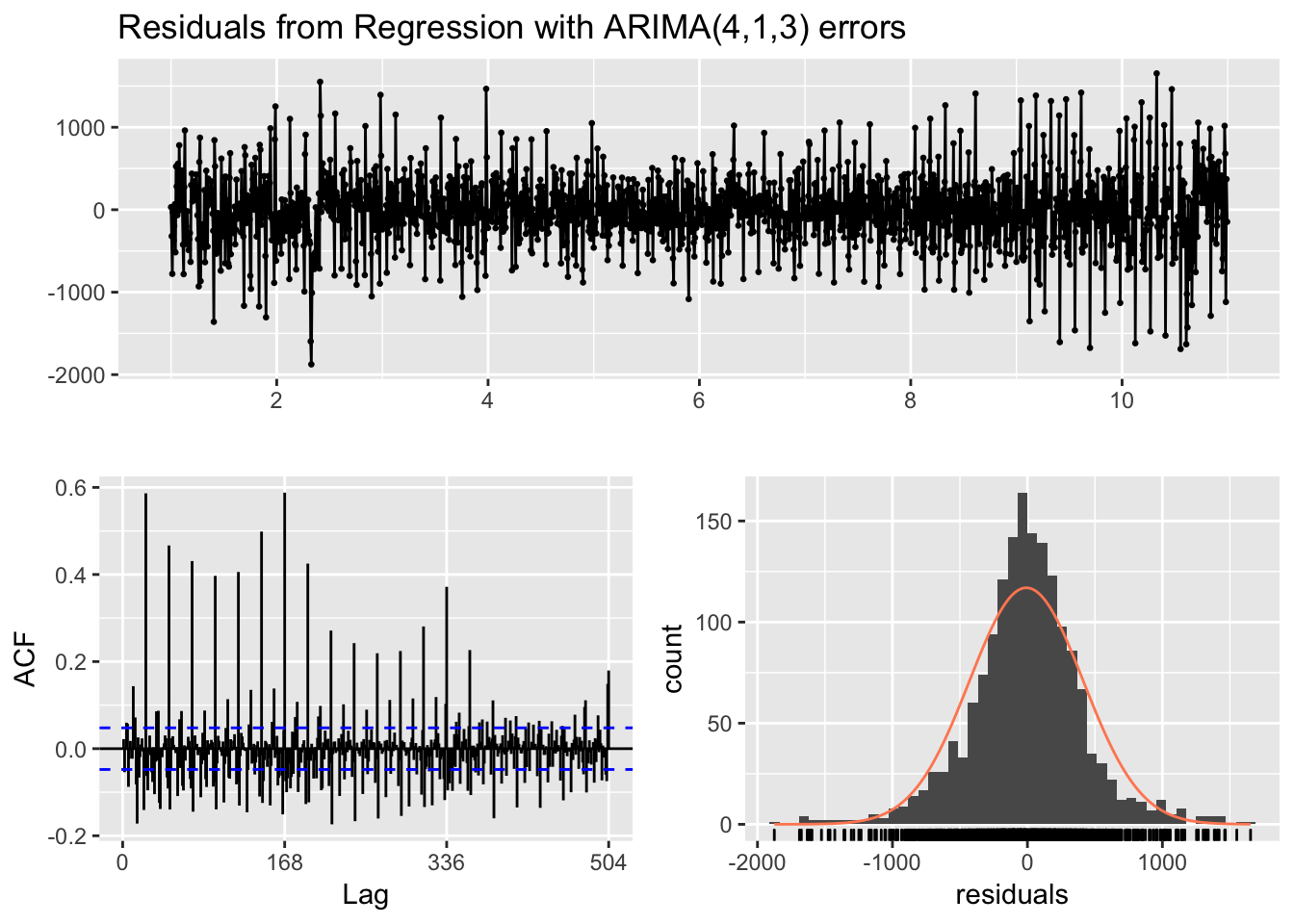
##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(4,1,3) errors
## Q* = 6405.9, df = 289, p-value < 2.2e-16
##
## Model df: 47. Total lags used: 336# Calculo error MAPE
MAPE_ARIMA_temperatura <- accuracy(forecast_regresores_total, testset_cov)Ahora sí parece que el error MAPE ha mejorado algo.
Comparativa de los 3 modelos
Comparando los 3 modelos, parece claro que aún queda margen de mejora con respecto a los valores reales de demanda eléctrica.
# Preparo tablas para graficar
fechas <- prevision_demanda %>% filter(as.Date(datetime) >= "2018-08-06 00:00:00",
as.Date(datetime) <= "2018-10-21 00:00:00")
fechas <- fechas[1671:1838, "datetime"]
resultados <- data.frame(real = testset_cov,
ARIMA_univariado = forecast_fourier$mean,
ARIMA_festivos = forecast_regresores$mean,
ARIMA_temperatura = forecast_regresores_total$mean,
datetime = fechas)
# Grafico comparación de las tres modelizaciones
ggplot(resultados, aes(x=datetime)) +
geom_line(aes(y = real, colour = "real")) +
geom_line(aes(y = ARIMA_univariado, colour = "ARIMA_univariado")) +
geom_line(aes(y = ARIMA_festivos, colour = "ARIMA_festivos")) +
geom_line(aes(y = ARIMA_temperatura, colour = "ARIMA_temperatura"))## Don't know how to automatically pick scale for object of type msts/ts. Defaulting to continuous.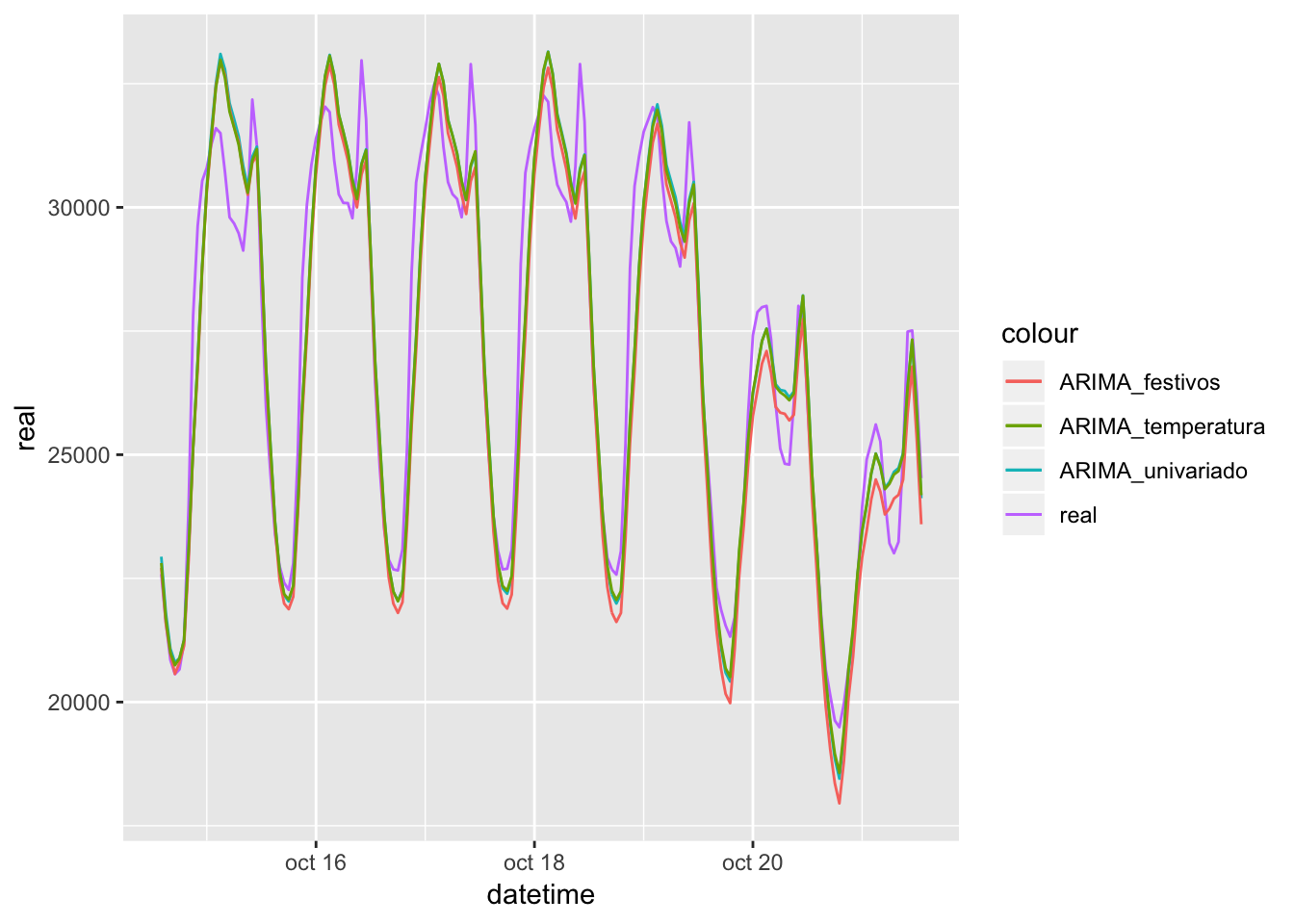
# Tabla de errores
list(MAPE_ARIMA_temperatura = MAPE_ARIMA_temperatura,
MAPE_ARIMA_festivos = MAPE_ARIMA_festivos,
MAPE_ARIMA_univariado = MAPE_ARIMA_univariado)## $MAPE_ARIMA_temperatura
## ME RMSE MAE MPE MAPE MASE
## Training set -7.868049 421.2048 307.0102 -0.04586708 1.084100 0.2246910
## Test set 173.495362 1122.5293 846.8061 0.63897969 3.016327 0.6197504
## ACF1 Theil's U
## Training set 0.02194579 NA
## Test set 0.79956834 0.8081229
##
## $MAPE_ARIMA_festivos
## ME RMSE MAE MPE MAPE MASE
## Training set -0.3111087 419.2958 308.6173 -0.01885757 1.092281 0.2258672
## Test set 490.5693809 1248.7418 974.1571 1.87119059 3.545390 0.7129545
## ACF1 Theil's U
## Training set 0.01566928 NA
## Test set 0.81087328 0.921001
##
## $MAPE_ARIMA_univariado
## ME RMSE MAE MPE MAPE MASE
## Training set -8.457158 421.8831 307.0658 -0.04808655 1.084365 0.2247317
## Test set 164.657071 1146.1321 875.0205 0.62158296 3.130744 0.6403996
## ACF1 Theil's U
## Training set 0.02208333 NA
## Test set 0.80638214 0.826702La modelización mediante series temporales es compleja, y bajo mi experiencia presenta resultados algo peores con respecto a algoritmos de machine learning con los datos del sector energético. Sin embargo, resulta fácil realizar una primera aproximación que dé unos valores sobre los que trabajar de manera rápida. Todo eso sí, depende de cada caso, ya que no sería lo mismo comenzar a realizar un forecast de clientes, por ejemplo, de una comercializadora en sus primeros años de vida, que hacerlo sobre una consolidada. Se requiere analizar cada momento de la serie temporal y valorar qué aproximación puede resultar óptima en cuanto a precisión-coste.